解:(1)由题意,设圆心坐标为(a,a+4)
∵半径为

的圆C经过坐标原点O
∴a
2+(a+4)
2=8
∴a
2+4a+4=0
∴a=-2
∴圆心坐标为(-2,2)
∴圆C的方程:(x+2)
2+(y-2)
2=8
(2)将直线l:x-y-m=0与圆C联立,消去y可得:2x
2-2mx+m
2+4m=0
设A(x
1,y
1),B(x
2,y
2),则x
1+x
2=m
∴y
1+y
2=x
1+x
2+2m=3m
∵线段AB的中点恰在抛物线x
2=4y上
∴
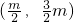
满足方程x
2=4y
∴
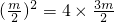
∴m=0或m=24
当m=0时,△=4m
2-8(m
2+4m)=0,不符合题意.
当m=24时,△=4m
2-8(m
2+4m)<0
所以不存在直线l:x-y-m=0与圆C交于不同的两点A,B,且线段AB的中点恰在抛物线x
2=4y上
分析:(1)由题意,设圆心坐标为(a,a+4),利用半径为

的圆C经过坐标原点O,可得a
2+(a+4)
2=8,从而可得圆心坐标,进而可求圆C的方程;
(2)将直线l:x-y-m=0与圆C联立,消去y可得:2x
2-2mx+m
2+4m=0.设A(x
1,y
1),B(x
2,y
2),则x
1+x
2=m
,y
1+y
2=x
1+x
2+2m=3m,利用线段AB的中点恰在抛物线x
2=4y上,可求得m=0或m=24,再验证△=4m
2-8(m
2+4m),即可知是否存在.
点评:本题考查的重点是圆的方程,考查直线与圆相交,解题时,将直线与圆联立是关键,判别式是否验证是易错点.

 的圆C经过坐标原点O.
的圆C经过坐标原点O. 的圆C经过坐标原点O
的圆C经过坐标原点O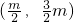 满足方程x2=4y
满足方程x2=4y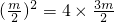
 的圆C经过坐标原点O,可得a2+(a+4)2=8,从而可得圆心坐标,进而可求圆C的方程;
的圆C经过坐标原点O,可得a2+(a+4)2=8,从而可得圆心坐标,进而可求圆C的方程;

 如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.
如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.