
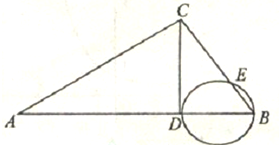
 如图∠ACB=90°,CD⊥AB于点D.以BD为直径的圆与BC交于点E.下面的结论正确的是
如图∠ACB=90°,CD⊥AB于点D.以BD为直径的圆与BC交于点E.下面的结论正确的是| CD |
| BD |
| AD |
| CD |


 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:高中数学 来源: 题型:
| a |
| b |
| a |
| b |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、即不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| A、递增数列 | B、递减数列 |
| C、常数列 | D、摆动数列 |
查看答案和解析>>
科目:高中数学 来源:2015届辽宁省高三上学期第一次模拟考试理科数学试卷(解析版) 题型:解答题
已知函数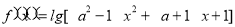 .设命题p:“
.设命题p:“ 的定义域为R”;命题q:“
的定义域为R”;命题q:“ 的值域为R”
的值域为R”
(1)分别求命题p、q为真时,实数a的取值范围;
(2)?p是q的什么条件?请说明理由.
查看答案和解析>>
科目:高中数学 来源:2015届辽宁省大连市高三上学期期中考试理科数学试卷(解析版) 题型:解答题
(不等式选讲)(本小题满分10分)设函数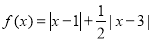
(1)求不等式 的解集;
的解集;
(2)若不等式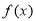
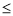
 的解集非空,求实数
的解集非空,求实数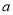 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com