
����Ŀ��ij��ҽ�Ʊ���ʵ�ж���ҽ���ƶȣ����ա��ͽ���ҽ�������������ԭ�μӱ�����Ա������ѡ���ļ�ҽ�Ʊ��ն���ҽԺ��һ������ҽԺ��Ϊ���˾����ҽ�ƻ��������ס��ҡ�������4���μӱ�����Ա���ڵ���������A��B��C��������ҽԺ���������ǵ�ѡ����������ģ�
������ס������˶�ѡ��A����ҽԺ�ĸ��ʣ�
������ס������˲�ѡ��ͬһ������ҽԺ�ĸ��ʣ�
������4���μӱ�����Ա��ѡ��A����ҽԺ������Ϊ�Σ���εķֲ��к���ѧ������
���𰸡��⣺�����衰�ס������˶�ѡ��A����ҽԺ��Ϊ�¼�A����ôP��A��= ![]() ��
�� ![]() =
= ![]() ���Լס������˶�ѡ��A����ҽԺ�ĸ���Ϊ
���Լס������˶�ѡ��A����ҽԺ�ĸ���Ϊ ![]() ��
��
�����衰�ס�������ѡ��ͬһ������ҽԺ��Ϊ�¼�B��
������A��B��C��������ҽԺ������P��B��=3�� ![]() ��
�� ![]() =
= ![]()
���Լס������˲�ѡ��ͬһ������ҽԺ�ĸ�����P�� ![]() ��=1��P��B��=
��=1��P��B��= ![]() ��
��
������������ο���ȡ��ֵΪ0��1��2��3��4����ô
P����=0��= ![]() =
= ![]() �� P����=1��=
�� P����=1��= ![]() =
= ![]() ��
��
P����=2��= ![]() =
= ![]() ��P����=3��=
��P����=3��= ![]() =
= ![]() ��P����=4��=
��P����=4��= ![]() =
= ![]()
���Ԧεķֲ���Ϊ
�� | 0 | 1 | 2 | 3 | 4 |
P |
|
|
|
|
|
E��=0�� ![]() +1��
+1�� ![]() +2��
+2�� ![]() +3��
+3�� ![]() +4��
+4�� ![]() =
= ![]()
�������������衰�ס������˶�ѡ��A����ҽԺ��Ϊ�¼�A���������ǵ�ѡ����������������ó˷���ʽ����������ס�������ѡ��ͬһ������ҽԺ���¼��ĸ��ʣ�����ס������˲�ѡ��ͬһ������ҽԺ�ĸ��ʣ�����ȷ����������ο���ȡ��ֵ��������Ӧ�ĸ��ʣ����ɵõ��εķֲ�������ѧ������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������̨���ϡ��µ���ı߳��ֱ���3��6�� 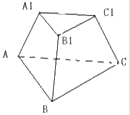
��1����������������ɵĽ�Ϊ60�㣬�������̨�������
��2����������������ɵĽ�Ϊ60�㣬�������̨�IJ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() .
.
��1�����ۺ���![]() �ĵ����ԣ�
�ĵ����ԣ�
��2����![]() ʱ��������
ʱ��������![]() �ĵ�����
�ĵ�����![]() ��ͼ����
��ͼ����![]() �ύ��
�ύ��![]() ��
�� ![]() ���㣬�������ֱ�Ϊ
���㣬�������ֱ�Ϊ![]() ��
�� ![]() ���߶�
���߶�![]() ���е�ĺ�����Ϊ
���е�ĺ�����Ϊ![]() ����
����![]() ��
�� ![]() ǡΪ����
ǡΪ����![]() ����㣬��֤��
����㣬��֤�� ![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��= 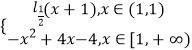
��1���ڸ���ֱ������ϵ��ֱ�ӻ���f��x���IJ�ͼ�������б���㣩������ͼ��д������ f��x���ĵ��������䣻 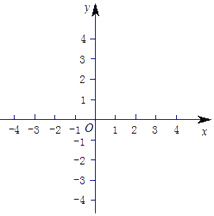
��2����mΪ��ֵʱf��x��+m=0��������ͬ����㣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ۼס���������Ʒ��������ֱ���y1 �� y2��Ԫ��������Ͷ���ʽ�x��Ԫ�Ĺ�ϵ�ֱ�Ϊy1=m ![]() +a��y2=bx��������m��a��b��Ϊ������������y1 �� y2��Ӧ������C1 �� C2��ͼ��ʾ��
+a��y2=bx��������m��a��b��Ϊ������������y1 �� y2��Ӧ������C1 �� C2��ͼ��ʾ�� 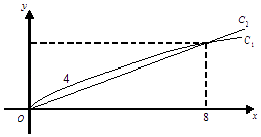
��1������y1��y2�Ľ���ʽ��
��2�������̳�һ��Ͷ��10��Ԫ�����ס���������Ʒ������̳�������������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x���ǣ����ޣ�0���ȣ�0��+�ޣ��ϵ��溯�����ҵ�x��0ʱ�������IJ���ͼ����ͼ��ʾ����ʽxf��x����0�Ľ⼯�ǣ� �� 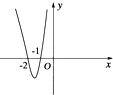
A.����2����1���ȣ�1��2��
B.����2����1���ȣ�0��1���ȣ�2��+�ޣ�
C.�����ޣ���2���ȣ���1��0���ȣ�1��2��
D.�����ޣ���2���ȣ���1��0���ȣ�0��1���ȣ�2��+�ޣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() ��������Ϊ
��������Ϊ![]() ���ҹ���
���ҹ��� ��
��
��1����![]() �ķ��̣�
�ķ��̣�
��2���Ƿ����ֱ��![]() ��
��![]() �ཻ��
�ཻ��![]() ���㣬�����㣺��
���㣬�����㣺��![]() ��
��![]() ��
��![]() Ϊ����ԭ�㣩��б��֮��Ϊ2����ֱ��
Ϊ����ԭ�㣩��б��֮��Ϊ2����ֱ��![]() ��Բ
��Բ![]() ���У������ڣ����
���У������ڣ����![]() �ķ��̣��������ڣ���˵�����ɣ�
�ķ��̣��������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ����Ӧ�������䲼�ġ������ƽ���Сѧ����ѧ���е��������ijУ�ƻ����������ѧ���пγ̣�����ȫУѧ����ѡ��������е���(����Ҫ��ȫԱ���룬ÿ��ѧ������Ӱ��ſγ���ѡ��Ψһһ�ſγ�).���ε���������.
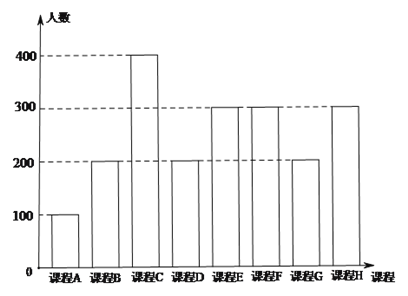
ͼ�У��γ�![]() Ϊ������γ̣��γ�
Ϊ������γ̣��γ�![]() Ϊ��Ȼ��ѧ��γ�.Ϊ��һ���о�ѧ��ѡ�����������ͼ������ȡ�ֲ����������ȫУ��ȡ1%��ѧ����Ϊ�о������飨���¼�ơ���
Ϊ��Ȼ��ѧ��γ�.Ϊ��һ���о�ѧ��ѡ�����������ͼ������ȡ�ֲ����������ȫУ��ȡ1%��ѧ����Ϊ�о������飨���¼�ơ���![]() ����.
����.
�����ڡ���![]() ���У�ѡ��������γ̺���Ȼ��ѧ��γ̵��������ж��٣�
���У�ѡ��������γ̺���Ȼ��ѧ��γ̵��������ж��٣�
����ij�ؾٰ���Ȼ��ѧӪ���ѧУҪ�μӻ��ѧ��ֻ���ǡ���![]() ����ѡ��
����ѡ��![]() ��
��
�̻�![]() �γ̵�ͬѧ��������Щͬѧ����Ը�����ɷѵķ�ʽ�μӻ. ѡ��
�γ̵�ͬѧ��������Щͬѧ����Ը�����ɷѵķ�ʽ�μӻ. ѡ��![]() �γ̵�ѧ������
�γ̵�ѧ������![]() �˲μӿ�ѧӪ���ÿ�������
�˲μӿ�ѧӪ���ÿ�������![]() Ԫ��ѡ��
Ԫ��ѡ��![]() �γ̵�ѧ������
�γ̵�ѧ������![]() �˲μӸû��ÿ�������
�˲μӸû��ÿ�������![]() Ԫ.��ѡ��
Ԫ.��ѡ��![]() �γ̺�
�γ̺�![]() �γ̵�ѧ����Ը�������������Ϊ
�γ̵�ѧ����Ը�������������Ϊ![]() ���μӻ��ѧ�����ɷ����ܺ�Ϊ
���μӻ��ѧ�����ɷ����ܺ�Ϊ![]() Ԫ.
Ԫ.
�ٵ�![]() ʱ��д��
ʱ��д��![]() �����п���ȡֵ��
�����п���ȡֵ��
����ѡ��![]() �γ̵�ͬѧ���μӿ�ѧӪ�����
�γ̵�ͬѧ���μӿ�ѧӪ�����![]() Ԫ�ĸ���.
Ԫ�ĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
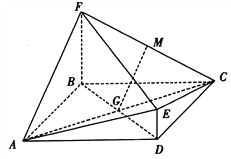
����Ŀ����ͼ����![]() ���ı���BDEF�ཻ��BD��
���ı���BDEF�ཻ��BD�� ![]() ƽ��ABCD��DE//BF,BF=2DE��AF��FC��MΪCF���е㣬
ƽ��ABCD��DE//BF,BF=2DE��AF��FC��MΪCF���е㣬 ![]() ��
��
(I)��֤��GM����ƽ��CDE��
(II)��֤��ƽ��ACE��ƽ��ACF��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com