
【题目】已知函数![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)当![]() 时,若函数
时,若函数![]() 的导函数
的导函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() ,
, ![]() 两点,其横坐标分别为
两点,其横坐标分别为![]() ,
, ![]() ,线段
,线段![]() 的中点的横坐标为
的中点的横坐标为![]() ,且
,且![]() ,
, ![]() 恰为函数
恰为函数![]() 的零点,求证:
的零点,求证: ![]() .
.
【答案】(1)当![]() 时,
时, ![]() 在
在![]() 内单调递增;当
内单调递增;当![]() 时,
时, ![]() 在
在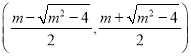 内单调递减,在
内单调递减,在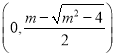 ,
, 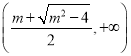 内单调递增;(2)见解析.
内单调递增;(2)见解析.
【解析】试题分析:(1)对函数求导后,利用导数与函数单调性的关系,对![]() 进行讨论可得函数单调性;(2)由函数的导函数可知,
进行讨论可得函数单调性;(2)由函数的导函数可知, ![]() 又是
又是![]() 的零点,代入相减化简得
的零点,代入相减化简得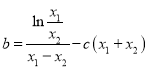 ,对
,对![]() 求导,
求导, ![]()
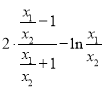 .令
.令![]() ,求得函数
,求得函数![]() .不等式得证.
.不等式得证.
试题解析:(1)由于![]() 的定义域为
的定义域为![]() ,则
,则![]() .对于方程
.对于方程![]() ,其判别式
,其判别式![]() .当
.当![]() ,即
,即![]() 时,
时, ![]() 恒成立,故
恒成立,故![]() 在
在![]() 内单调递增.当
内单调递增.当![]() ,即
,即![]() ,方程
,方程![]() 恰有两个不相等是实
恰有两个不相等是实![]() ,令
,令![]() ,得
,得![]() 或
或![]() ,此时
,此时![]() 单调递增;令
单调递增;令![]() ,得
,得![]() ,此时
,此时![]() 单调递减.
单调递减.
综上所述,当![]() 时,
时, ![]() 在
在![]() 内单调递增;当
内单调递增;当![]() 时,
时, ![]() 在
在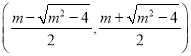 内单调递减,在
内单调递减,在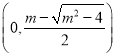 ,
, 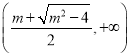 内单调递增.
内单调递增.
(2)由(1)知, ![]() ,所以
,所以![]() 的两根
的两根![]() ,
, ![]() 即为方程
即为方程![]() 的两根.因为
的两根.因为![]() ,所以
,所以![]() ,
, ![]() ,
, ![]() .又因为
.又因为![]() ,
, ![]() 为
为![]() 的零点,
的零点,
所以![]() ,
, ![]() ,两式相减得
,两式相减得![]() ,得
,得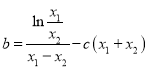 .而
.而![]() ,所以
,所以![]()
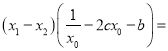
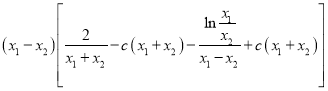
![]()
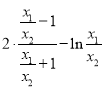 .
.
令![]() ,由
,由![]() 得
得![]() ,因为
,因为![]() ,两边同时除以
,两边同时除以![]() ,得
,得![]() ,因为
,因为![]() ,故
,故![]() ,解得
,解得![]() 或
或![]() ,所以
,所以![]() .设
.设![]() ,所以
,所以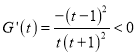 ,则
,则![]() 在
在![]() 上是减函数,所以
上是减函数,所以![]() ,
,
即![]() 的最小值为
的最小值为![]() .
.
所以![]() .
.


科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知极坐标系的极点为直角坐标系![]() 的原点,极轴为
的原点,极轴为![]() 轴的正半轴,两种坐标系中的长度单位相同,圆
轴的正半轴,两种坐标系中的长度单位相同,圆![]() 的直角坐标方程为
的直角坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),射线
为参数),射线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求圆![]() 和直线
和直线![]() 的极坐标方程;
的极坐标方程;
(2)已知射线![]() 与圆
与圆![]() 的交点为
的交点为![]() ,与直线
,与直线![]() 的交点为
的交点为![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() +
+ ![]()
(1)将函数f(x)化简成Asin(ωx+φ)+B(A>0,φ>0,φ∈[0,2π))的形式;
(2)求f(x)的单调递减区间,并指出函数|f(x)|的最小正周期;
(3)求函数f(x)在[ ![]() ,
, ![]() ]上的最大值和最小值.
]上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】利用简单随机抽样从某小区抽取100户居民进行月用电量调查,发现其用电量都在50到350度之间,频率分布直方图如图所示.在这些用户中,用电量落在区间[150,250]内的户数为( ) 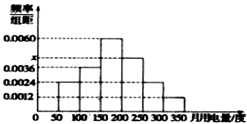
A.46
B.48
C.50
D.52
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市医疗保险实行定点医疗制度,按照“就近就医、方便管理”的原则,参加保险人员可自主选择四家医疗保险定点医院和一家社区医院作为本人就诊的医疗机构.若甲、乙、丙、丁4名参加保险人员所在地区附近有A,B,C三家社区医院,并且他们的选择是相互独立的.
(Ⅰ)求甲、乙两人都选择A社区医院的概率;
(Ⅱ)求甲、乙两人不选择同一家社区医院的概率;
(Ⅲ)设4名参加保险人员中选择A社区医院的人数为ξ,求ξ的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com