【题目】已知 
=（1，2）， 
=（﹣3，2），当k为何值时：
（1）k + 与 ﹣3 垂直；
（2）k + 与 ﹣3 平行，平行时它们是同向还是反向？
【答案】
（1）解：由题意可得 k 
+ 
=（k﹣3，2k+2）， ﹣3 =（10，﹣4），
由 k + 与 ﹣3 垂直可得 （k﹣3，2k+2）（10，﹣4）=10（k﹣3）+（2k+2）（﹣4）=0，解得k=19．
（2）解：由 k + 与 ﹣3 平行，可得（k﹣3）（﹣4）﹣（2k+2）×10=0，解得k=﹣ 
，
此时，k + =﹣ + =（﹣ 
， 
）， ﹣3 =（10，﹣4），显然k + 与 ﹣3 方向相反．
【解析】（1）由题意可得 k + 和 ﹣3 的坐标，由 k + 与 ﹣3 垂直可得它们的数量积等于 0，由此解得k的值．（2）由 k + 与 ﹣3 平行的性质，可得（k﹣3）（﹣4）﹣（2k+2）×10=0，解得k的值．再根据 k + 和 ﹣3 的坐标，可得k + 与 ﹣3 方向相反．
阅读快车系列答案科目：高中数学 来源： 题型：
【题目】已知点
，点
是圆
上的任意一点，设
为该圆的圆心，并且线段
的垂直平分线与直线
交于点
.
（1）求点
的轨迹方程；
（2）已知
两点的坐标分别为
， 
，点
是直线
上的一个动点，且直线
分别交（1）中点
的轨迹于
两点（
四点互不相同），证明：直线
恒过一定点，并求出该定点坐标.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】将函数y=sin2x的图象向左平移 
个单位，再向上平移1个单位，所得图象的函数解析式是（ ）
A.y=cos2x
B.y=2cos2x
C.
D.y=2sin2x?
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】正三棱台的上、下底面的边长分别是3和6．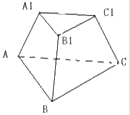 
（1）若侧面与底面所成的角为60°，求此三棱台的体积；
（2）若侧棱与底面所成的角为60°，求此三棱台的侧面积．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
.
（1）讨论函数
的单调性；
（2）当
时，若函数
的导函数
的图象与
轴交于
， 
两点，其横坐标分别为
， 
，线段
的中点的横坐标为
，且
， 
恰为函数
的零点，求证： 
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
