
分析 利用根与系数的关系得出{an}的递推公式,从而得出an,bn的通项公式,在解不等式得出n的值.
解答 解:∵an+1、1+an是函数f(x)=x2-bnx+an的两个零点,
∴an+1(1+an)=an,即an+1=$\frac{{a}_{n}}{1+{a}_{n}}$,
∴$\frac{1}{{a}_{n+1}}$-$\frac{1}{{a}_{n}}$=1,又a1=1,
∴{$\frac{1}{{a}_{n}}$}是以1为首项,以1为公差的等差数列.
∴$\frac{1}{{a}_{n}}$=n,即an=$\frac{1}{n}$,∴a2=$\frac{1}{2}$,
又由根与系数的关系得:bn=an+1+(1+an)=$\frac{1}{n}+\frac{1}{n+1}$+1,
令$\frac{1}{n}+\frac{1}{n+1}$+1>$\frac{4}{3}$,得n2-5n-3<0,解得$\frac{5-\sqrt{37}}{2}$<n<$\frac{5+\sqrt{37}}{2}$,
又n∈N,故n的最大值为5.
故答案为:$\frac{1}{2}$,5.
点评 本题考查了数列的通项公式的求法,等差数列的判断,属于中档题.


 计算高手系列答案
计算高手系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ±$\frac{\sqrt{3}}{3}$ | B. | -$\frac{\sqrt{3}}{3}$ | C. | ±$\sqrt{3}$ | D. | -$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 存在实数x0,使得g(x0)=1 | B. | 当x1<x2时,必有g(x1)<g(x2) | ||
| C. | g(2)的取值与实数a有关 | D. | 函数g(f(x))的图象必过定点 |
查看答案和解析>>
科目:高中数学 来源:2016-2017学年河北省高二理上第一次月考数学试卷(解析版) 题型:解答题
(1)用辗转相除法求228与1995的最大公约数.
(2)用秦九韶算法求多项式f(x)=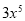 +
+ -8x+5在x=2时的值。
-8x+5在x=2时的值。
查看答案和解析>>
科目:高中数学 来源:2016-2017学年河北省高二理上第一次月考数学试卷(解析版) 题型:选择题
一个球体经过切割后,剩下部分几何体的三视图如右图所示,则剩下部分几何体的体积为( )
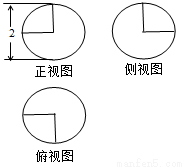
A.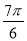 B.
B.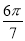 C.
C.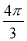 D.
D.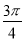
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com