已知函数f(x)=2|x-m|和函数g(x)=x|x-m|+2m-8.
(1)若m=2,求函数f(x)的单调区间;
(2)若对任意x1∈(-∞,4],均存在x2∈[4,+∞),使得f(x1)=g(x2)成立,求实数m的取值范围.
解:(1)m=2时,函数f(x)=)=2
|x-2|,故函数f(x)的单调增区间为(2,+∞),单调减区间为(-∞,2);
(2)f(x)=
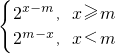
,则f(x)的值域应是g(x)的值域的子集.
①当4≤m≤8时,f(x)在(-∞,4]上单调减,故f(x)≥f(4)=2
m-4 ,
g(x)在[4,m]上单调减,[m,+∞)上单调增,故g(x)≥g(m)=2m-8,
所以2
m-4≥2m-8,解得4≤m≤5或8≥m≥6.
②当m>8时,f(x)在(-∞,4]上单调减,故f(x)≥f(4)=2
m-4,g(x)在[4,

]单调增,[

,m]上单调减,[m,+∞)上单调增,g(4)=6m-24>g(m)=2m-8,
故g(x)≥g(m)=2m-8,所以2
m-4≥2m-8,解得m≥8
③0<m<4时,f(x)在(-∞,m]上单调减,[m,4]上单调增,故f(x)≥f(m)=1.
g(x)在[4,+∞)上单调增,故g(x)≥g(4)=8-2m,所以8-2m≤1,即

≤m<4.
④m≤0时,f(x)在(-∞,m]上单调减,在[m,4]上单调增,故f(x)≥f(m)=1.
g(x)在[4,+∞)上单调增,故g(x)≥g(4)=8-2m,所以8-2m≤1,即m≥

.(舍去)
综上,m的取值范围是[

,5]∪[6,+∞).
分析:(1)m=2时,函数f(x)=)=2
|x-2|,由此可得函数的单调区间;
(2)由题意可得f(x)的值域应是g(x)的值域的子集,再分4≤m≤8、m>8、0<m<4、m≤0四种情况,分别求出实数m的取值范围,再取并集即得所求.
点评:本题主要考查函数的单调性的判断,利用函数的单调性求函数的最值,体现了分类讨论的数学思想,属于中档题.

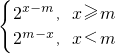 ,则f(x)的值域应是g(x)的值域的子集.
,则f(x)的值域应是g(x)的值域的子集. ]单调增,[
]单调增,[ ,m]上单调减,[m,+∞)上单调增,g(4)=6m-24>g(m)=2m-8,
,m]上单调减,[m,+∞)上单调增,g(4)=6m-24>g(m)=2m-8, ≤m<4.
≤m<4. .(舍去)
.(舍去) ,5]∪[6,+∞).
,5]∪[6,+∞).

 全程金卷系列答案
全程金卷系列答案 快乐5加2金卷系列答案
快乐5加2金卷系列答案