
(本题满分14分)已知二次函数 满足
满足 且
且 .
.
(Ⅰ)求 的解析式.
的解析式.
(Ⅱ)在区间 上,
上,  的图象恒在
的图象恒在 的图象上方,试确定实数
的图象上方,试确定实数 的范围.
的范围.
(Ⅰ)f(x)=x2-x+1.(Ⅱ)m<-1
【解析】
试题分析:(Ⅰ)由待定系数法可设f(x)=ax2+bx+c( ), 由f(0)=1得c=1,故f(x)=ax2+bx+1.又因为f(x+1)-f(x)=2x,代入可得a(x+1)2+b(x+1)+1-(ax2+bx+1)=2x.即2ax+a+b=2x, 所以
), 由f(0)=1得c=1,故f(x)=ax2+bx+1.又因为f(x+1)-f(x)=2x,代入可得a(x+1)2+b(x+1)+1-(ax2+bx+1)=2x.即2ax+a+b=2x, 所以 ∴f(x)=x2-x+1.
∴f(x)=x2-x+1.
(Ⅱ)由题意 的图象恒在
的图象恒在 的图象上方即x2-x+1>2x+m在[-1,1]上恒成立,即x2-3x+1-m>0在[-1,1]上恒成立.令g(x)= x2-3x+1-m,其图象的对称轴为直线x=
的图象上方即x2-x+1>2x+m在[-1,1]上恒成立,即x2-3x+1-m>0在[-1,1]上恒成立.令g(x)= x2-3x+1-m,其图象的对称轴为直线x= ,所以g(x) 在[-1,1]上递减.
,所以g(x) 在[-1,1]上递减.
所以g(1)>0,即12-3×1+1-m>0,从而m<-1.
试题解析: (Ⅰ)设f(x)=ax2+bx+c,由f(0)=1得c=1,故f(x)=ax2+bx+1. 2分
∵f(x+1)-f(x)=2x,∴a(x+1)2+b(x+1)+1-(ax2+bx+1)=2x.
即2ax+a+b=2x, 4分
所以 , 6分∴f(x)=x2-x+1. 7分
, 6分∴f(x)=x2-x+1. 7分
(Ⅱ)由题意得x2-x+1>2x+m在[-1,1]上恒成立.即x2-3x+1-m>0在[-1,1]上恒成立.
设g(x)= x2-3x+1-m,其图象的对称轴为直线x= , 9分
, 9分
所以g(x) 在[-1,1]上递减.
故只需g(1)>0, 即12-3×1+1-m>0, 12分
解得m<-1. 14分
考点:待定系数法求函数解析式及二次函数性质的应用.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:2014-2015学年广东省高一9月综合检测数学试卷(解析版) 题型:选择题
如图所示,液体从一圆锥形漏斗漏入一圆柱形桶中,开始时,漏斗盛满液体,经过3分钟漏完.已知圆柱中液面上升的速度是一个常量,H是圆锥形漏斗中液面下落的距离,则H与下落时间t(分)的函数关系表示的图象只可能是
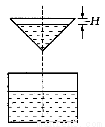
 A. B. C. D.
A. B. C. D.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省高一第一次月考数学试卷(解析版) 题型:选择题
若 ,规定:
,规定: ,例如:( )
,例如:( )
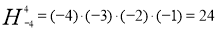 ,则
,则 的奇偶性为
的奇偶性为
A.是奇函数不是偶函数
B.是偶函数不是奇函数
C.既是奇函数又是偶函数
D.既不是奇函数又不是偶函数
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省高一第一次月考数学试卷(解析版) 题型:选择题
设a , b∈R , 集合{ a , 1 } = { 0, a + b } , 则b – a = ( )
A.1 B.-1 C.2 D.-2
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省高一10月月考数学试卷(解析版) 题型:选择题
不等式2x2﹣x﹣1>0的解集是( )
A.
B.(1,+∞)
C.(﹣∞,1)∪(2,+∞)
D. ∪(1,+∞)
∪(1,+∞)
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省高一上学期第一次阶段考试数学试卷(解析版) 题型:选择题
若函数 在区间(-∞,2
在区间(-∞,2 上是减函数,则实数
上是减函数,则实数 的取值范围是( )
的取值范围是( )
A. -
- ,+∞) B.(-∞,-
,+∞) B.(-∞,-
 C.
C.
 ,+∞) D.(-∞,
,+∞) D.(-∞,

查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省高二上学期期初考试理数学卷(解析版) 题型:选择题
在 中,角
中,角 的对边分别为
的对边分别为 ,向量
,向量 ,
, ,
,
若 ,且
,且 ,则角
,则角 ,
, 的大小为( ).
的大小为( ).
A. ,
, B.
B. ,
, C.
C. ,
, D.
D. ,
,
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com