Question

【题目】设数列{an}的前n项和为Sn ， 且（Sn﹣1）2=anSn（n∈N*）．
（1）求S1 ， S2 ， S3的值；
（2）求出Sn及数列{an}的通项公式；
（3）设bn=（﹣1）n﹣1（n+1）2anan+1（n∈N*），求数列{bn}的前n项和为Tn ．

Answer 1

【答案】
（1）解：∵（Sn﹣1）2=anSn（n∈N*），

∴n≥2时，（Sn﹣1）2=（Sn﹣Sn﹣1）Sn（n∈N*）．

∴n=1时， ，解得a1= =S1．

n=2时， ，解得S2= ．

同理可得：S3=

（2）解：由（1）可得：n≥2时，（Sn﹣1）2=（Sn﹣Sn﹣1）Sn（n∈N*）．

化为：Sn= ．（*）

猜想Sn= ．

n≥2时，代入（*），左边= ；右边= = ，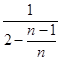

∴左边=右边，猜想成立，n=1时也成立．

∴n≥2时，an=Sn﹣Sn﹣1= ﹣ = ，n=1时也成立．

∴Sn= ，an=

（3）解：bn=（﹣1）n﹣1（n+1）2anan+1（n∈N*）=（﹣1）n﹣1 =（﹣1）n﹣1 ，

∴n=2k（k∈N*）时，数列{bn}的前n项和为

Tn= ﹣ + +…+ ﹣

= = ﹣ ．

n=2k﹣1（k∈N*）时，数列{bn}的前n项和为

Tn= ﹣ + +…﹣ +

= = + ．

∴Tn= ×

【解析】（1）由（Sn﹣1）2=anSn（n∈N*），分别取n=1，2，3即可得出．（2）由（1）可得：n≥2时，（Sn﹣1）2=（Sn﹣Sn﹣1）Sn（n∈N*）．化为：Sn= ．猜想Sn= ．代入验证即可得出．（3）bn=（﹣1）n﹣1（n+1）2anan+1（n∈N*）=（﹣1）n﹣1 =（﹣1）n﹣1 ，对n分类讨论，利用“裂项求和”方法即可得出．
【考点精析】关于本题考查的数列的前n项和和数列的通项公式，需要了解数列{an}的前n项和sn与通项an的关系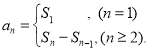；如果数列an的第n项与n之间的关系可以用一个公式表示，那么这个公式就叫这个数列的通项公式才能得出正确答案．