
【题目】已知数列![]() 中,
中,![]() ,且
,且![]() .
.
(1)求证:![]() 是等比数列,并求数列
是等比数列,并求数列![]() 的通项公式;
的通项公式;
(2)数列![]() 中是否存在不同的三项按照一定顺序重新排列后,构成等差数列?若存在,求满足条件的项;若不存在,说明理由.
中是否存在不同的三项按照一定顺序重新排列后,构成等差数列?若存在,求满足条件的项;若不存在,说明理由.
【答案】(1)证明见解析,![]() ;(2)不存在.
;(2)不存在.
【解析】
(1)推导出an+1+1=﹣3(an+1),n∈N*.a1+1=2,由此能证明{an+1}是以2为首项,﹣3为公比的等比数列,可求数列{an}通项公式.(2)假设am,an,ap构成等差数列,m≠n≠p,则2an=am+ap,利用(1)的通项公式进行推导不满足2an=am+ap,从而数列{an}中不存在不同的三项按照一定顺序重新排列后,构成等差数列.
(1)因为![]() ,所以
,所以![]() ,因为
,因为![]() ,
,
所以数列![]() 是以2为首项,以-3为公比的等比数列,
是以2为首项,以-3为公比的等比数列,
所以![]() ,即
,即![]() ;
;
(2)假设存在三项![]() 按一定顺序重新排列后成等差.
按一定顺序重新排列后成等差.
①若![]() ,则
,则![]() ,
,
整理得![]() ,两边同除以
,两边同除以![]() ,
,
可得![]() ,
,
等式右边是-3的整数倍,左边不是-3的整数倍,故等式不成立.
②若![]() ,则
,则![]() ,
,
整理得![]() ,两边同除以
,两边同除以![]() ,
,
可得![]() ,
,
等式右边是-3的整数倍,左边不是-3的整数倍,故等式不成立.
③若![]() ,则
,则![]() ,
,
整理得![]() ,两边同除以
,两边同除以![]() ,
,
可得![]() ,
,
等式左边是-3的整数倍,右边不是-3的整数倍,故等式不成立;
综上,不存在不同的三项符合题意.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】如图,某公园内有一块矩形绿地区域ABCD,已知AB=100米,BC=80米,以AD,BC为直径的两个半圆内种植花草,其它区域种值苗木. 现决定在绿地区域内修建由直路BN,MN和弧形路MD三部分组成的观赏道路,其中直路MN与绿地区域边界AB平行,直路为水泥路面,其工程造价为每米2a元,弧形路为鹅卵石路面,其工程造价为每米3a元,修建的总造价为W元. 设![]() .
.
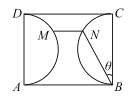
(1)求W关于![]() 的函数关系式;
的函数关系式;
(2)如何修建道路,可使修建的总造价最少?并求最少总造价.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次恶劣气候的飞行航程中调查男女乘客在飞机上晕机的情况,共调查了89位乘客,其中男乘客有24人晕机,31人不晕机;女乘客有8人晕机,26人不晕机
(1)根据此材料数据完成如下的2×2列联表;
晕机 | 不晕机 | 总计 | |
男人 | |||
女人 | |||
总计 |
(2)根据列联表,利用下列公式和数据分析,你是否有90%的把握认为在本次飞机飞行中晕机与性别有关?
(3)其中8名晕机的女乘客中有5名是常坐飞机的乘客,另外3名是不常坐飞机的,从这8名乘客中任选3名,这3名乘客不都是常坐飞机的概率是多少?
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
参考公式: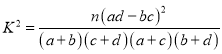 ,其中
,其中![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,以坐标原点O为极点,x轴正半轴为极轴建立极坐标系。已知曲线C的极坐标方程为![]() ,过点
,过点![]() 的直线l的参数方程为
的直线l的参数方程为 (为参数),直线l与曲线C交于M、N两点。
(为参数),直线l与曲线C交于M、N两点。
(1)写出直线l的普通方程和曲线C的直角坐标方程:
(2)若![]() 成等比数列,求a的值。
成等比数列,求a的值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有![]() ,
,![]() ,…,
,…,![]() 这5个球队进行单循环比赛(全部比赛过程中任何一队都要分别与其他各队比赛一场且只比赛一场).当比赛进行到一定阶段时,统计
这5个球队进行单循环比赛(全部比赛过程中任何一队都要分别与其他各队比赛一场且只比赛一场).当比赛进行到一定阶段时,统计![]() ,
,![]() ,
,![]() ,
,![]() 这4个球队已经赛过的场数分别为:
这4个球队已经赛过的场数分别为:![]() 队4场,
队4场,![]() 队3场,
队3场, ![]() 队2场,
队2场,![]() 队1场,则
队1场,则![]() 队比赛过的场数为( )
队比赛过的场数为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定点![]() ,定直线
,定直线![]() :
: ![]() ,动圆
,动圆![]() 过点
过点![]() ,且与直线
,且与直线![]() 相切.
相切.
(Ⅰ)求动圆![]() 的圆心轨迹
的圆心轨迹![]() 的方程;
的方程;
(Ⅱ)过点![]() 的直线与曲线
的直线与曲线![]() 相交于
相交于![]() ,
, ![]() 两点,分别过点
两点,分别过点![]() ,
, ![]() 作曲线
作曲线![]() 的切线
的切线![]() ,
, ![]() ,两条切线相交于点
,两条切线相交于点![]() ,求
,求![]() 外接圆面积的最小值.
外接圆面积的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com