
分析 根据正切函数的性质得出不等式解出即可.
解答 解:y=-tan(x+$\frac{π}{6}$)+2的周期T=π.
由函数有意义得:x+$\frac{π}{6}$≠$\frac{π}{2}+kπ$,解得x≠$\frac{π}{3}+kπ$.∴y=-tan(x+$\frac{π}{6}$)+2的定义域是{x|x≠$\frac{π}{3}+kπ$,k∈Z}.
令-$\frac{π}{2}+kπ$<x+$\frac{π}{6}$$<\frac{π}{2}+kπ$,解得-$\frac{2π}{3}+kπ$<x<$\frac{π}{3}+kπ$,∴y=-tan(x+$\frac{π}{6}$)+2的单调区间为(-$\frac{2π}{3}+kπ$,$\frac{π}{3}+kπ$),k∈Z.
点评 本题考查了正切函数的图象与性质,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{5}$ | B. | 4$\sqrt{5}$ | C. | 12 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4an=1-3Sn | B. | 4Sn=3an-1 | C. | 4Sn=3an+1 | D. | 4an=3Sn+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
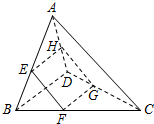 如图,在四面体A-BCD中,AC与BD互相垂直,且长度分别为2和3,平行于这两条棱的平面与边AB、BC、CD、DA分别相交于点E、F、G、H,记四边形EFGH的面积为y,设$\frac{BE}{AB}$=x,则( )
如图,在四面体A-BCD中,AC与BD互相垂直,且长度分别为2和3,平行于这两条棱的平面与边AB、BC、CD、DA分别相交于点E、F、G、H,记四边形EFGH的面积为y,设$\frac{BE}{AB}$=x,则( )| A. | 函数f(x)的值域为(0,1] | B. | 函数y=f(x)满足f(x)=f(2-x) | ||
| C. | 函数y=f(x)的最大值为2 | D. | 函数y=f(x)在(0,$\frac{1}{2}$)上单调递增 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com