
| 1 | 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 140 |
| 9 |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年鹰潭市二模文)(12分)在中央电视台所举办的北京2008年奥运会火炬手的一期选拔节目中,假定每个选手需要进行四轮考核,每轮设有一个问题,能正确回答者进入下一轮考核,否则被淘汰,已知某选手能正确回答第一、二、三、四轮问题的概率分别为![]() ,且各轮问题能否正确回答互不影响。
,且各轮问题能否正确回答互不影响。
(1)求该选手进入第四轮才被淘汰的概率;
(2)求该选手至多进入第三轮考核的概率;
查看答案和解析>>
科目:高中数学 来源: 题型:
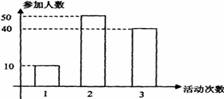
令人瞩目的2008年奥运会即将在中国举行,为了迎接这次奥运盛会,成都市从某中学选出100名优秀学生代表,在举行奥运会之前每人至少参加一次社会公益活动,他们参加活动的次数统计如图所示。
(Ⅰ)求100名优秀学生代表参加活动的人均次数。
(Ⅱ)从100名优秀学生代表中任选两名,求他们参加活动次数恰好相等的概率。
(Ⅲ)从100名优秀学生代表中任选两名,求这两人参加活动次数之差的绝对值不小于1的概率。
查看答案和解析>>
科目:高中数学 来源:2011-2012学年高二(上)期末数学试卷(文科)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com