
【题目】已知函数![]() .
.
(1)若函数![]() 的图象在点
的图象在点![]() 处的切线的斜率为
处的切线的斜率为![]() ,求函数
,求函数![]() 在
在![]() 上的最小值;
上的最小值;
(2)若关于![]() 的方程
的方程![]() 在
在![]() 上有两个解,求实数
上有两个解,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)先求![]() ,导数的几何意义求解
,导数的几何意义求解![]() ,利用导数求函数的最值,即可.
,利用导数求函数的最值,即可.
(2)由题意可知![]() ,若使得关于
,若使得关于![]() 的方程
的方程![]() 在
在![]() 上有两个解,则需
上有两个解,则需![]() 在
在![]() 有两个解. 令
有两个解. 令![]() ,
,![]() ,利用导数研究函数的极值与最值,令
,利用导数研究函数的极值与最值,令![]() ,求解即可.
,求解即可.
(1)由题意可知,![]() ,
,
则![]() ,即
,即![]() ,
,
故![]() ;
;
令![]() ,即
,即![]() ;
;
当![]() 时
时![]() ,
,![]() 在
在![]() 上单调递减.
上单调递减.
当![]() 时
时![]() ,
,![]() 在
在![]() 上单调递增.
上单调递增.
因为![]() ,
,![]() ,
,![]()
所以![]()
故函数![]() 在
在![]() 上的最小值为
上的最小值为![]() .
.
(2)依题意,![]() ;
;
若使得关于![]() 的方程
的方程![]() 在
在![]() 上有两个解
上有两个解
则需![]() 在
在![]() 有两个解.
有两个解.
令![]() ,
,![]() .
.
①当![]() 时,
时,![]()
所以![]() 在
在![]() 上单调递增.
上单调递增.
由零点存在性定理,![]() 在
在![]() 至多一个零点,不符合题意舍去.
至多一个零点,不符合题意舍去.
②当![]() 时,令
时,令![]() ,则
,则![]() .
.
|
|
|
|
|
| 0 |
|
| 单调递增 | 极大值 | 单调递减 |
因为![]() ,
,![]() ,
,
所以要使![]() 在
在![]() 内有两个零点,
内有两个零点,
则![]() 即可,即
即可,即![]() ,
,
又因为![]() ,所以
,所以![]()
综上所述,实数![]() 的取值范围为
的取值范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 和圆
和圆![]() ,倾斜角为45°的直线
,倾斜角为45°的直线![]() 过抛物线
过抛物线![]() 的焦点,且
的焦点,且![]() 与圆
与圆![]() 相切.
相切.
(1)求![]() 的值;
的值;
(2)动点![]() 在抛物线
在抛物线![]() 的准线上,动点
的准线上,动点![]() 在
在![]() 上,若
上,若![]() 在
在![]() 点处的切线
点处的切线![]() 交
交![]() 轴于点
轴于点![]() ,设
,设![]() .求证点
.求证点![]() 在定直线上,并求该定直线的方程.
在定直线上,并求该定直线的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》中有一分鹿问题:“今有大夫、不更、簪袅、上造、公士,凡五人,共猎得五鹿.欲以爵次分之,问各得几何.”在这个问题中,大夫、不更、簪袅、上造、公士是古代五个不同爵次的官员,现皇帝将大夫、不更、簪枭、上造、公士这5人分成两组(一组2人,一组3人),派去两地执行公务,则大夫、不更恰好在同一组的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,曲线C1的参数方程为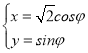 (
(![]() 为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为
为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为![]() ,曲线C2的极坐标方程为ρ=2sinθ.
,曲线C2的极坐标方程为ρ=2sinθ.
(1)探究直线l与曲线C2的位置关系,并说明理由;
(2)若曲线C3的极坐标方程为![]() ,且曲线C3与曲线C1、C2分别交于M、N两点,求|OM|2|ON|2的取值范围.
,且曲线C3与曲线C1、C2分别交于M、N两点,求|OM|2|ON|2的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,上、下顶点分别为
,上、下顶点分别为![]() ,若
,若![]() ,点
,点![]() 关于直线
关于直线![]() 的对称点在椭圆
的对称点在椭圆![]() 上.
上.
(1)求椭圆![]() 的方程与离心率;
的方程与离心率;
(2)过点![]() 做直线
做直线![]() 与椭圆
与椭圆![]() 相交于两个不同的点
相交于两个不同的点![]() ;若
;若![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,某班一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损,其中,频率分布直方图的分组区间分别为![]() ,据此解答如下问题.
,据此解答如下问题.
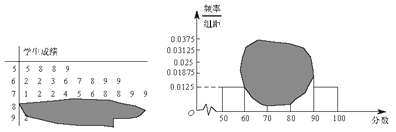
(Ⅰ)求全班人数及分数在![]() 之间的频率;
之间的频率;
(Ⅱ)现从分数在![]() 之间的试卷中任取 3 份分析学生情况,设抽取的试卷分数在
之间的试卷中任取 3 份分析学生情况,设抽取的试卷分数在![]() 的份数为
的份数为![]() ,求
,求![]() 的分布列和数学望期.
的分布列和数学望期.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,的焦点为
,的焦点为![]() ,过点
,过点![]() 的直线
的直线![]() 的斜率为
的斜率为![]() ,与抛物线
,与抛物线![]() 交于
交于![]() ,
,![]() 两点,抛物线在点
两点,抛物线在点![]() ,
,![]() 处的切线分别为
处的切线分别为![]() ,
,![]() ,两条切线的交点为
,两条切线的交点为![]() .
.
(1)证明:![]() ;
;
(2)若![]() 的外接圆
的外接圆![]() 与抛物线
与抛物线![]() 有四个不同的交点,求直线
有四个不同的交点,求直线![]() 的斜率的取值范围.
的斜率的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com