
【题目】如图,在四棱锥![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() ≌
≌![]() ,
,![]() ,
,![]() 是线段
是线段![]() 的中点.
的中点.
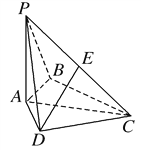
(1)求证:![]() ∥平面
∥平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:![]() 建立空间直角坐标系,给出相应点坐标,得平面PAB的法向量为
建立空间直角坐标系,给出相应点坐标,得平面PAB的法向量为![]() ,由
,由![]() ,即可得
,即可得![]() ∥平面
∥平面![]()
![]() 求出平面
求出平面![]() 的一个法向量,平面
的一个法向量,平面![]() 的法向量,利用向量的夹角公式,即可求出二面角
的法向量,利用向量的夹角公式,即可求出二面角![]() 的余弦值;
的余弦值;
解析:(1)证明:以B为坐标原点,BA所在的直线为x轴,BC所在的直线为y轴,过点B且与平面ABC垂直的直线为z轴,建立空间直角坐标系如图所示.
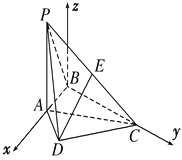
则B(0,0,0),C(0,![]() ,0),P(1,0,2),D
,0),P(1,0,2),D![]() ,A(1,0,0),E
,A(1,0,0),E![]() ,∴
,∴![]() ,
,![]() ,
,![]() .
.
显然平面PAB的法向量为![]() ,由
,由![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() ∥平面
∥平面![]() .
.
(2)由(1)知![]() ,
,![]() ,
,![]() ,设平面
,设平面![]() 的法向量为
的法向量为![]() ,则
,则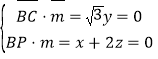 ,取
,取![]() ,则
,则![]() ,∴
,∴![]() 为平面
为平面![]() 的一个法向量.同理:平面
的一个法向量.同理:平面![]() 的法向量为
的法向量为![]()
∴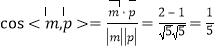 ,故二面角
,故二面角![]() 的余弦值为
的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知数列{an}的各项均为正数,满足a1=1,ak+1﹣ak=ai . (i≤k,k=1,2,3,…,n﹣1)
(1)求证: ![]() ;
;
(2)若{an}是等比数列,求数列{an}的通项公式;
(3)设数列{an}的前n项和为Sn , 求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设抛物线C:x2=2py(p>0)的焦点为F,准线为l,A∈C,已知以F为圆心,FA为半径的圆F交l于B,D两点;
(1)若∠BFD=90°,△ABD的面积为 ![]() ,求p的值及圆F的方程;
,求p的值及圆F的方程;
(2)若A,B,F三点在同一直线m上,直线n与m平行,且n与C只有一个公共点,求坐标原点到m,n距离的比值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设a<1,集合A={x∈R|x>0},B={x∈R|2x2﹣3(1+a)x+6a>0},D=A∩B.
(1)求集合D(用区间表示);
(2)求函数f(x)=2x3﹣3(1+a)x2+6ax在D内的极值点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学在一次研究性学习中发现,以下五个式子的值都等于同一个常数.
1)sin213°+cos217°﹣sin13°cos17°
2)sin215°+cos215°﹣sin15°cos15°
3)sin218°+cos212°﹣sin18°cos12°
4)sin2(﹣18°)+cos248°﹣sin2(﹣18°)cos48°
5)sin2(﹣25°)+cos255°﹣sin2(﹣25°)cos55°
(Ⅰ)试从上述五个式子中选择一个,求出这个常数;
(Ⅱ)根据(Ⅰ)的计算结果,将该同学的发现推广为三角恒等式,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4﹣4:坐标系与参数方程
在平面直角坐标系中,以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系.已知直线l上两点M,N的极坐标分别为(2,0),( ![]() ),圆C的参数方程
),圆C的参数方程 ![]() (θ为参数).
(θ为参数).
(Ⅰ)设P为线段MN的中点,求直线OP的平面直角坐标方程;
(Ⅱ)判断直线l与圆C的位置关系.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三国魏人刘徽,自撰《海岛算经》,专论测高望远.其中有一题:今有望海岛,立两表齐,高三丈,前後相去千步,令後表与前表相直。从前表却行一百二十三步,人目著地取望岛峰,与表末参合。从後表却行百二十七步,人目著地取望岛峰,亦与表末参合。问岛高及去表各几何?翻译如下:要测量海岛上一座山峰![]() 的高度
的高度![]() ,立两根高三丈的标杆
,立两根高三丈的标杆![]() 和
和![]() ,前后两竿相距
,前后两竿相距![]() 步,使后标杆杆脚
步,使后标杆杆脚![]() 与前标杆杆脚
与前标杆杆脚![]() 与山峰脚
与山峰脚![]() 在同一直线上,从前标杆杆脚
在同一直线上,从前标杆杆脚![]() 退行
退行![]() 步到
步到![]() ,人眼著地观测到岛峰,
,人眼著地观测到岛峰,![]() 、
、![]() 、
、![]() 、三点共线,从后标杆杆脚
、三点共线,从后标杆杆脚![]() 退行
退行![]() 步到
步到![]() ,人眼著地观测到岛峰,
,人眼著地观测到岛峰,![]() 、
、![]() 、
、![]() 三点也共线,则山峰的高度
三点也共线,则山峰的高度![]() __________步.(古制
__________步.(古制![]() 步
步![]() 尺,
尺,![]() 里
里![]() 丈
丈![]() 尺
尺![]() 步)
步)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工艺品厂要设计一个如图1所示的工艺品,现有某种型号的长方形材料如图2所示,其周长为4m,这种材料沿其对角线折叠后就出现图1的情况.如图,ABCD(AB>AD)为长方形的材料,沿AC折叠后AB'交DC于点P,设△ADP的面积为S2 , 折叠后重合部分△ACP的面积为S1 .
(Ⅰ)设AB=xm,用x表示图中DP的长度,并写出x的取值范围;
(Ⅱ)求面积S2最大时,应怎样设计材料的长和宽?
(Ⅲ)求面积(S1+2S2)最大时,应怎样设计材料的长和宽?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x+ ![]() |﹣|x﹣
|﹣|x﹣ ![]() |;
|;
(1)作出函数f(x)的图象;
(2)根据(1)所得图象,填写下面的表格:
性质 | 定义域 | 值域 | 单调性 | 奇偶性 | 零点 |
f(x) |
(3)关于x的方程f2(x)+m|f(x)|+n=0(m,n∈R)恰有6个不同的实数解,求n的取值范围. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com