设等差数列{an}的前n项的和为Sn,且S4=-62,S6=-75,求:
(1){an}的通项公式an 及前n项的和Sn;
(2)|a1|+|a2|+|a3|+…+|a14|.
解:(1)设等差数列{a
n}的公差为d,依题意得
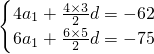
,解得a
1=-20,d=3.
∴a
n=-20+(n-1)×3=3n-23;
S
n=
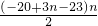
=

n
2-
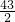
n.
(2)∵a
n=3n-23,
∴由a
n<0得n<8,
∴|a
1|+|a
2|+|a
3|+…+|a
14|=-a
1-a
2-…-a
7+a
8+…+a
14=S
14-2S
7=

×14
2-
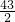
×14-2(

×7
2-
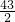
×7)
=7(42-43)-7(21-43)
=-7-7×(-22)
=147.
分析:(1)由S
4=-62,S
6=-75,可得到等差数列{a
n}的首项a
1与公差d的方程组,解之即可求得{a
n}的通项公式a
n 及前n项的和S
n;
由(1)可知a
n,由a
n<0得n<8,从而|a
1|+|a
2|+|a
3|+…+|a
14|=S
14-2S
7,计算即可.
点评:本题考查数列的求和,着重考查等差数列的通项公式与前n项和公式,考查解方程组的能力,求得a
n是关键,属于中档题.

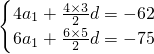 ,解得a1=-20,d=3.
,解得a1=-20,d=3.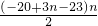 =
= n2-
n2-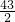 n.
n. ×142-
×142-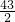 ×14-2(
×14-2( ×72-
×72-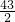 ×7)
×7)
