
已知函数f(x)= ,x∈[-1,1],函数g(x)=[f(x)]2-2af(x)+3的最小值为h(a).
,x∈[-1,1],函数g(x)=[f(x)]2-2af(x)+3的最小值为h(a).
(1)求h(a);
(2)是否存在实数m、n同时满足下列条件:
①m>n>3;
②当h(a)的定义域为[n,m]时,值域为[n2,m2]?若存在,求出m、n的值;若不存在,说明理由.
(1)h(a)= (2)不存在
(2)不存在
【解析】(1)∵x∈[-1,1],∴f(x)=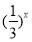 ∈
∈ .设t=
.设t=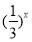 ,t∈
,t∈ ,
,
则y=φ(t)=t2-2at+3=(t-a)2+3-a2.
当a<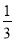 时,ymin=h(a)=φ
时,ymin=h(a)=φ =
= ;
;
当 ≤a≤3时,ymin=h(a)=φ(a)=3-a2;
≤a≤3时,ymin=h(a)=φ(a)=3-a2;
当a>3时,ymin=h(a)=φ(3)=12-6a.
∴h(a)=
(2)假设满足题意的m、n存在,∵m>n>3,∴h(a)=12-6a在(3,+∞)上是减函数.∵h(a)的定义域为[n,m],值域为[n2,m2],∴ ,由②-①得6(m-n)=(m-n)(m+n),∵m>n>3,∴m+n=6,但这与“m>n>3”矛盾,∴满足题意的m、n不存在.
,由②-①得6(m-n)=(m-n)(m+n),∵m>n>3,∴m+n=6,但这与“m>n>3”矛盾,∴满足题意的m、n不存在.


 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案科目:高中数学 来源:2014年高考数学(理)二轮复习6-1直线与圆练习卷(解析版) 题型:选择题
当直线l:y=k(x-1)+2被圆C:(x-2)2+(y-1)2=5截得的弦最短时,k的值为( ).
A.2 B. 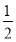 C.3 D.1
C.3 D.1
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习3-2解三角形练习卷(解析版) 题型:解答题
在△ABC中,角A,B,C所对的边分别是a,b,c,设平面向量e1= ,e2=
,e2= ,且e1⊥e2.
,且e1⊥e2.
(1)求cos 2A的值;
(2)若a=2,求△ABC的周长L的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习2-2导数及其应用练习卷(解析版) 题型:填空题
由直线x=-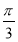 ,x=
,x=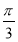 ,y=0与曲线y=cos x所围成的封闭图形的面积为________.
,y=0与曲线y=cos x所围成的封闭图形的面积为________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习2-1函数的概念与基本初等函数练习卷(解析版) 题型:选择题
设f(x)与g(x)是定义在同一区间[a,b]上的两个函数,若函数y=f(x)-g(x)在x∈[a,b]上有两个不同的零点,则称f(x)和g(x)在[a,b]上是“关联函数”,区间[a,b]称为“关联区间”.若f(x)=x2-3x+4与g(x)=2x+m在[0,3]上是“关联函数”,则m的取值范围是 ( ).
A. 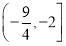 B.[-1,0] C.(-∞,-2] D.
B.[-1,0] C.(-∞,-2] D. 
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习1-2算法与程序框图等练习卷(解析版) 题型:填空题
(a+x)(1+  )5的展开式中x2项的系数是15,则展开式的所有项系数的和是________.
)5的展开式中x2项的系数是15,则展开式的所有项系数的和是________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮专题复习知能提升演练选修4-5练习卷(解析版) 题型:选择题
若关于x的不等式|x-2|+|x-a|≥a在R上恒成立,则a的最大值是( ).
A.0 B.1 C.-1 D.2
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮专题复习知能提升演练1-7-2练习卷(解析版) 题型:解答题
设袋子中装有a个红球,b个黄球,c个蓝球,且规定:取出一个红球得1分,取出一个黄球得2分,取出一个蓝球得3分.
(1)当a=3,b=2,c=1时,从该袋子中任取(有放回,且每球取到的机会均等)2个球,记随机变量ξ为取出此2球所得分数之和,求ξ的分布列;
(2)从该袋子中任取(每球取到的机会均等)1个球,记随机变量η为取出此球所得分数.若E(η)= ,D(η)=
,D(η)= ,求a∶b∶c.
,求a∶b∶c.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com