
【题目】已知抛物线C:y2=4x与椭圆E:![]() 1(a>b>0)有一个公共焦点F.设抛物线C与椭圆E在第一象限的交点为M.满足|MF|
1(a>b>0)有一个公共焦点F.设抛物线C与椭圆E在第一象限的交点为M.满足|MF|![]() .
.
(1)求椭圆E的标准方程;
(2)过点P(1,![]() )的直线交抛物线C于A、B两点,直线PO交椭圆E于另一点Q.若P为AB的中点,求△QAB的面积.
)的直线交抛物线C于A、B两点,直线PO交椭圆E于另一点Q.若P为AB的中点,求△QAB的面积.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)由抛物线的定义可得![]() ,则M(
,则M(![]() ,
,![]() ),再由椭圆的定义可得
),再由椭圆的定义可得![]() ,即可求得
,即可求得![]() ,进而求解;
,进而求解;
(2)设A(x1,y1),B(x2,y2),利用斜率公式可得![]() ,即可得到直线AB的方程,再由点到直线距离可得点
,即可得到直线AB的方程,再由点到直线距离可得点![]() 到直线
到直线![]() 的距离
的距离![]() ,联立抛物线和直线
,联立抛物线和直线![]() ,进而利用弦长公式求得
,进而利用弦长公式求得![]() ,则
,则![]() ,即可求解.
,即可求解.
(1)由抛物线方程可得F(1,0),则椭圆的另一个焦点![]() ,
,
因为![]() ,∴M(
,∴M(![]() ,
,![]() ),
),
则2a 4,则a=2,
4,则a=2,
所以![]() ,
,
所以椭圆E的标准方程为![]() .
.
(2)设A(x1,y1),B(x2,y2),点P(1,![]() )在椭圆上,则Q(﹣1,
)在椭圆上,则Q(﹣1,![]() ),
),
因为P为AB的中点,且 ,
,
则kAB![]() ,
,
故直线AB的方程为y![]() (x﹣1),即8x﹣6y+1=0,
(x﹣1),即8x﹣6y+1=0,
∴Q到直线AB的距离 ,
,
联立![]() ,整理得64x2﹣128x+1=0,
,整理得64x2﹣128x+1=0,
故x1+x2=2,x1x2![]() ,
,
则![]() ,
,
所以![]()
![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点.

(Ⅰ)证明: BC1//平面A1CD;
(Ⅱ)设AA1= AC=CB=2,AB=2![]() ,求三棱锥C一A1DE的体积.
,求三棱锥C一A1DE的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着经济的发展,个人收入的提高,自2019年1月1日起,个人所得税起征点和税率的调整.调整如下:纳税人的工资、薪金所得,以每月全部收入额减除5000元后的余额为应纳税所得额.依照个人所得税税率表,调整前后的计算方法如下表:
个人所得税税率表(调整前) | 个人所得税税率表(调整后) | ||||
免征额3500元 | 免征额5000元 | ||||
级数 | 全月应纳税所得额 | 税率(%) | 级数 | 全月应纳税所得额 | 税率(%) |
1 | 不超过1500元部分 | 3 | 1 | 不超过3000元部分 | 3 |
2 | 超过1500元至4500元的部分 | 10 | 2 | 超过3000元至12000元的部分 | 10 |
3 | 超过4500元至9000元的部分 | 20 | 3 | 超过12000元至25000元的部分 | 20 |
... | ... | ... | ... | ... | ... |
(1)假如小红某月的工资、薪金等所得税前收入总和不高于8000元,记![]()
![]() 表示应纳的税,试写出调整前后
表示应纳的税,试写出调整前后![]() 关于
关于![]() 的函数表达式;
的函数表达式;
(2)某税务部门在小红所在公司利用分层抽样方法抽取某月100个不同层次员工的税前收入,并制成下面的频数分布表:
收入(元) |
|
|
|
|
|
|
人数 | 30 | 40 | 10 | 8 | 7 | 5 |
先从收入在![]() 及
及![]() 的人群中按分层抽样抽取7人,再从中选2人作为新纳税法知识宣讲员,求两个宣讲员不全是同一收入人群的概率;
的人群中按分层抽样抽取7人,再从中选2人作为新纳税法知识宣讲员,求两个宣讲员不全是同一收入人群的概率;
(3)小红该月的工资、薪金等税前收入为7500元时,请你帮小红算一下调整后小红的实际收入比调整前增加了多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 表示k个数字均为1的十进制数(如
表示k个数字均为1的十进制数(如![]() =1,
=1,![]() =111),定义
=111),定义![]() 。
。
(1)对于任意正整数m、n,令![]() ,写出一个关于f(m,n)的递推关系式,并证明之;
,写出一个关于f(m,n)的递推关系式,并证明之;
(2)证明:对于任意正整数m、n,{m+n}!均可以被{m}!.{n}!整除。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从广安市某中学校的![]() 名男生中随机抽取
名男生中随机抽取![]() 名测量身高,被测学生身高全部介于
名测量身高,被测学生身高全部介于![]() cm和
cm和![]() cm之间,将测量结果按如下方式分成八组:第一组
cm之间,将测量结果按如下方式分成八组:第一组![]() ,第二组
,第二组![]() ,...,第八组
,...,第八组![]() ,如图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为
,如图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为![]() 人.
人.
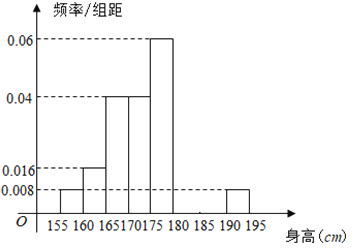
(1)求第七组的频率;
(2)估计该校![]() 名男生的身高的中位数。
名男生的身高的中位数。
(3)若从样本中身高属于第六组和第八组的所有男生中随机抽取两名男生,求抽出的两名男生是同一组的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com