
分析 先利用函数关系式,结合经过6个小时过虑还剩80%的污染物,即可求出k;P0e-kt≤51.2%P0可化为:${e}^{\frac{t}{6}ln0.8}$≤0.512,解得答案.
解答 解:由题意,经过6个小时过虑还剩80%的污染物,
∵P=P0e-kt,
∴80%P0=P0e-6k,
∴k=-$\frac{1}{6}$ln0.8;
∴P0e-kt≤51.2%P0可化为:${e}^{\frac{t}{6}ln0.8}$≤0.512,
则${0.8}^{\frac{t}{6}}$≤0.512=0.83,
即t≥18
即为了使剩余污染物不高于51.2%,则至少需要18小时
点评 本题考查函数模型的运用,考查学生的计算能力,属于中档题.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)+f(-x)=0 | B. | f(x)-f(-x)=0 | C. | $\frac{f(-x)}{f(x)}=-1$ | D. | $\frac{f(-x)}{f(x)}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
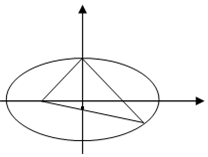 如图,F1,F2分别是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点,A是椭圆C的上顶点,B是直线AF2与椭圆C的另一个交点,∠F1AF2=60°
如图,F1,F2分别是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点,A是椭圆C的上顶点,B是直线AF2与椭圆C的另一个交点,∠F1AF2=60°查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com