
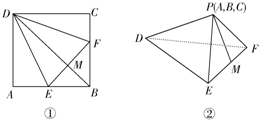
 如图,在正方形ABCD中,E,F分别是AB,BC的中点,现在沿DE,DF及EF把△ADE,△CDF和△BEF折起,使A,B,C三点重合,重合后的点记作P,那么在四面体P-DEF中必有( )
如图,在正方形ABCD中,E,F分别是AB,BC的中点,现在沿DE,DF及EF把△ADE,△CDF和△BEF折起,使A,B,C三点重合,重合后的点记作P,那么在四面体P-DEF中必有( )| A、DP⊥平面PEF |
| B、DM⊥平面PEF |
| C、PM⊥平面DEF |
| D、PF⊥平面DEF |
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com