
【题目】设函数f(x)=|ex﹣a|+| ![]() ﹣1|,其中a,x∈R,e是自然对数的底数,e=2.71828…
﹣1|,其中a,x∈R,e是自然对数的底数,e=2.71828…
(1)当a=0时,解不等式f(x)<2;
(2)求函数f(x)的单调增区间;
(3)设a≥ ![]() ,讨论关于x的方程f(f(x))=
,讨论关于x的方程f(f(x))= ![]() 的解的个数.
的解的个数.
【答案】
(1)解:当a=0时,不等式f(x)<2,即: ![]() ,
,
即 ![]() ,因此
,因此 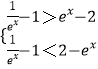
得 ![]() ,所以
,所以 ![]() ,
,
所以原不等式的解集为 ![]() .
.
(2)解:①当a≤0时, 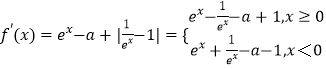
因为x>0时, ![]() ,x<0时,
,x<0时, ![]() ,
,
故f(x)在区间(﹣∞,0)上单调递减,在区间(0,+∞)上单调递增;…(5分)
②当0<a<1时, 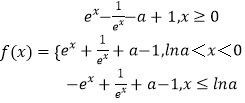 ,
,
仿①得f(x)在(﹣∞,lna)和(lna,0)上单调递减,在(0,+∞)上单调递增,
即f(x)在区间(﹣∞,0)上单调递减,在区间(0,+∞)上单调递增;(6分)
③当a=1时, 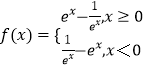
易得f(x)在区间(﹣∞,0)上单调递减,在区间(0,+∞)上单调递增; …(7分)
④当a>1时, 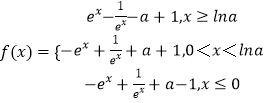
同理得f(x)在区间(﹣∞,lna)上单调递减,在区间(lna,+∞)上单调递增.…(8分)
综上所述,
当a≤1时,f(x)在区间(﹣∞,0)上单调递减,在区间(0,+∞)上单调递增;
当a>1时,f(x)在区间(﹣∞,lna)上单调递减,在区间(lna,+∞)上单调递增.…(10分)
(3)解:由(2)知:当 ![]() 时,因为
时,因为 ![]() ,
,
又x→+∞时, ![]() ,
,
所以f(x)的值域为 ![]() ,且
,且 ![]() (等号仅当
(等号仅当 ![]() 时取).)
时取).)
令 ![]() ,
,
当 ![]() 时,
时, ![]() ,所以
,所以 ![]() 不成立,原方程无解;
不成立,原方程无解;
当 ![]() 时,由
时,由 ![]() 得
得 ![]() ,因为
,因为 ![]() ,所以
,所以 ![]() ,
,
所以 ![]() 有两个不相等的实数根,故原方程有两个不同的实数解.
有两个不相等的实数根,故原方程有两个不同的实数解.
综上所述,当 ![]() 时,原方程无解;当
时,原方程无解;当 ![]() 时,原方程有两个不同的实数解.
时,原方程有两个不同的实数解.
【解析】(1)将a=0代入不等式,得到关于x的不等式组,解出即可;(2)通过讨论a的范围,求出f(x)的分段函数,从而求出函数的单调区间;(3)先求出函数的值域,结合换元法以及a的范围,求出方程的解即可.
【考点精析】掌握绝对值不等式的解法是解答本题的根本,需要知道含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号.


 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() 为实常数.
为实常数.
(Ⅰ)设![]() ,当
,当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(Ⅱ)当![]() 时,直线
时,直线![]() 、
、![]() 与函数
与函数![]() 、
、![]() 的图象一共有四个不同的交点,且以此四点为顶点的四边形恰为平行四边形.
的图象一共有四个不同的交点,且以此四点为顶点的四边形恰为平行四边形.
求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司生产甲、乙两种桶装产品.已知生产甲产品1桶需耗![]() 原料1千克、
原料1千克、![]() 原料2千克;生产乙产品1桶需耗
原料2千克;生产乙产品1桶需耗![]() 原料2千克,
原料2千克, ![]() 原料1千克.每桶甲产品的利润是300元,每桶乙产品的利润是400元.公司在生产这两种产品的计划中,要求每天消耗
原料1千克.每桶甲产品的利润是300元,每桶乙产品的利润是400元.公司在生产这两种产品的计划中,要求每天消耗![]() 原料都不超过12千克.通过合理安排生产计划,从每天生产的甲、乙两种产品中,公司共可获得的最大利润是__________元.
原料都不超过12千克.通过合理安排生产计划,从每天生产的甲、乙两种产品中,公司共可获得的最大利润是__________元.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“微信运动”已成为当下热门的健身方式,小王的微信朋友圈内也有大量好友参与了“微信运动”,他随机选取了其中的40人(男、女各20人),记录了他们某一天的走路步数,并将数据整理如下:
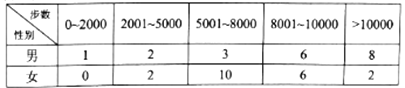
(1)若采用样本估计总体的方式,试估计小王的所有微信好友中每日走路步数超过5000步的概率;
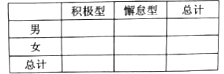
(2)已知某人一天的走路步数超过8000步被系统评定“积极型”,否则为“懈怠型”,根据题意完成下面的![]() 列联表,并据此判断能否有95%以上的把握认为“评定类型”与“性别”有关?
列联表,并据此判断能否有95%以上的把握认为“评定类型”与“性别”有关?
 附:
附: 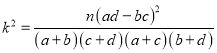 ,
,
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知,圆C:x2+y2﹣8y+12=0,直线l:ax+y+2a=0.
(1)当a为何值时,直线l与圆C相切;
(2)当直线l与圆C相交于A、B两点,且AB=2 ![]() 时,求直线l的方程.
时,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的焦点在
的焦点在![]() 轴上,椭圆
轴上,椭圆![]() 的左顶点为
的左顶点为![]() ,斜率为
,斜率为![]() 的直线交椭圆
的直线交椭圆![]() 于
于![]() ,
, ![]() 两点,点
两点,点![]() 在椭圆
在椭圆![]() 上,
上, ![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() .
.
(Ⅰ)当点![]() 为椭圆的上顶点,
为椭圆的上顶点, ![]() 的面积为
的面积为![]() 时,求椭圆的离心率;
时,求椭圆的离心率;
(Ⅱ)当![]() ,
, ![]() 时,求
时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com