
| A. | (0,1) | B. | (1,2) | C. | (1,+∞) | D. | (2,+∞) |
分析 令辅助函数F(x)=$\frac{f(x)}{x}$,求其导函数,据导函数的符号与函数单调性的关系判断出F(x)的单调性,利用单调性判断出由不等式 $\frac{f(\frac{1}{x})}{\frac{1}{x}}$>$\frac{f(x)}{x}$的关系,利用不等式的性质得到结论.
解答 解:令F(x)=$\frac{f(x)}{x}$,(x>0),
则F′(x)=$\frac{xf′(x)-f(x)}{{x}^{2}}$,
∵f(x)>xf′(x),∴F′(x)<0,
∴F(x)为定义域上的减函数,
由不等式x2f($\frac{1}{x}$)-f(x)>0,
得:$\frac{f(\frac{1}{x})}{\frac{1}{x}}$>$\frac{f(x)}{x}$,
∴$\frac{1}{x}$<x,∴x>1,
故选:C.
点评 本题考查了导数的运算,考查了利用导数研究函数单调性,函数的导函数符号确定函数的单调性:当导函数大于0时,函数单调递增;导函数小于0时,函数单调递减.此题为中档题.


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
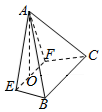 如图,在四棱锥A-EFCB中,△AEF为等边三角形,平面AEF⊥平面EFCB,BC=4,EF=2,四边形EFCB是高为$\sqrt{3}$的等腰梯形,EF∥BC,O为EF的中点.
如图,在四棱锥A-EFCB中,△AEF为等边三角形,平面AEF⊥平面EFCB,BC=4,EF=2,四边形EFCB是高为$\sqrt{3}$的等腰梯形,EF∥BC,O为EF的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知在四棱锥S-ABCD中,底面ABCD是边长为2的棱形,∠ABC=60°,侧面SAD为正三角形,侧面SAD⊥底面ABCD,E为线段AD的中点.
如图,已知在四棱锥S-ABCD中,底面ABCD是边长为2的棱形,∠ABC=60°,侧面SAD为正三角形,侧面SAD⊥底面ABCD,E为线段AD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 因为y=2x是指数函数,所以函数y=2x经过定点(0,1) | |
| B. | 猜想数列$\frac{1}{1×2}$,$\frac{1}{2×3}$,$\frac{1}{3×4}$,…的通项公式为an=$\frac{1}{n(n+1)}$(n∈N*) | |
| C. | 由“平面内垂直于同一直线的两直线平行”类比推出“空间中垂直于同一平面的两平面平行” | |
| D. | 由平面直角坐标系中圆的方程为(x-a)2+(y-b)2=r2,推测空间直角坐标系中球的方程为(x-a)2+(y-b)2+(z-c)2=r2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,高为3的直三棱柱ABC-A1B1C1中,底面是直角三角形,AC=2,D为A1C1的中点,F在线段AA1上,$\overrightarrow{CF}•\overrightarrow{D{B}_{1}}$=0,且A1F=1.
如图,高为3的直三棱柱ABC-A1B1C1中,底面是直角三角形,AC=2,D为A1C1的中点,F在线段AA1上,$\overrightarrow{CF}•\overrightarrow{D{B}_{1}}$=0,且A1F=1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-1] | B. | [-1,+∞) | C. | (-∞,1] | D. | [1,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com