
| A. | (-∞,-1] | B. | [-1,+∞) | C. | (-∞,1] | D. | [1,+∞) |
分析 讨论x=0时,不等式恒成立;x>0时,可得a≤$\frac{(x+1)ln(x+1)}{x}$恒成立.由$\frac{(x+1)ln(x+1)}{x}$-1=$\frac{(x+1)ln(x+1)-x}{x}$,令f(x)=(x+1)ln(x+1)-x,x>0,求得导数,判断单调性,即可得到a的范围.
解答 解:当x=0时,不等式(x+1)ln(x+1)≥ax显然成立;
当x>0时,不等式即为a≤$\frac{(x+1)ln(x+1)}{x}$恒成立.
由$\frac{(x+1)ln(x+1)}{x}$-1=$\frac{(x+1)ln(x+1)-x}{x}$,
令f(x)=(x+1)ln(x+1)-x,x>0,
导数为f′(x)=ln(x+1)+1-1=ln(x+1),
当x>0时,x+1>1,即有ln(x+1)>0.
即有f(x)在(0,+∞)递增,可得f(x)>f(0)=0,
即有$\frac{(x+1)ln(x+1)}{x}$>1,
则a≤1.即a的取值范围是(-∞,1].
故选:C.
点评 本题考查不等式恒成立问题的解法,注意运用参数分离和构造函数法,运用导数判断单调性是解题的关键,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (1,2) | C. | (1,+∞) | D. | (2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
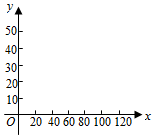 在某产品表面进行腐蚀刻度线实验,得到腐蚀深度y与腐蚀时间x之间相应的一组观察值如表:
在某产品表面进行腐蚀刻度线实验,得到腐蚀深度y与腐蚀时间x之间相应的一组观察值如表:| x(s) | 5 | 10 | 15 | 20 | 30 | 40 | 50 | 60 | 70 | 90 | 120 |
| y(μm) | 6 | 10 | 10 | 13 | 16 | 17 | 19 | 23 | 25 | 29 | 46 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| AQI | 0~50 | 51~100 | 101~150 | 151~200 | 201~300 | >300 |
| 级别 | Ⅰ级 | Ⅱ级 | Ⅲ级 | Ⅳ级 | Ⅴ级 | Ⅵ级 |
| 类别 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
| AQI指数 | 900 | 700 | 300 | 100 |
| 空气可见度 (千米) | 0.5 | 3.5 | 6.5 | 9.5 |
| AQI指数 | [0,200] | (201,400] | (401,600] | (601,800] | (801,1000] |
| 频数 | 3 | 6 | 12 | 6 | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\widehat{y}$=x-1 | B. | $\widehat{y}$=2x+1 | C. | $\widehat{y}$=x+2 | D. | $\widehat{y}$=x+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若求得相关系数r=-0.89,则y与x具备很强的线性相关关系,且为负相关 | |
| B. | 同学甲根据这组数据得到的回归模型1的残差平方和E1=1.8,同学乙根据这组数据得到的回归模型2的残差平方和E2=2.4,则模型1的拟合效果更好 | |
| C. | 用相关指数R2来刻画回归效果,模型1的相关指数R12=0.48,模型2的相关指数R22=0.91,则模型1的拟合效果更好 | |
| D. | 该回归分析只对被调查样本的总体适用 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com