
| AQI | 0��50 | 51��100 | 101��150 | 151��200 | 201��300 | ��300 |
| ���� | �� | �� | �� | ���� | ���� | ���� |
| ��� | �� | �� | �����Ⱦ | �ж���Ⱦ | �ض���Ⱦ | ������Ⱦ |
| AQIָ�� | 900 | 700 | 300 | 100 |
| �����ɼ��� ��ǧ�ף� | 0.5 | 3.5 | 6.5 | 9.5 |
| AQIָ�� | [0��200] | ��201��400] | ��401��600] | ��601��800] | ��801��1000] |
| Ƶ�� | 3 | 6 | 12 | 6 | 3 |
���� ��1�����ù�ʽ�������Իع鷽��ϵ�������ɵõ�y����x�����Իع鷽�̣�
��2���������ɱ�2֪AQIָ��������200��Ƶ��Ϊ0.1��AQIָ����200��400��Ƶ��Ϊ0.2��AQIָ������400��Ƶ��Ϊ0.7��ȷ������ÿ��������ȡֵ�����ʣ��Ӷ�����ֲ��м���ѧ������
�������ɣ�����������������ϴ�������벻����1200Ԫ����1A2C��3B��2B1C��1B2C��3C������������������С��������������ϴ����������벻����1200Ԫ�ĸ��ʣ�
��� �⣺��1��$\overline x=\frac{9+7+3+1}{4}=5$��$\overline y=\frac{0.5+3.5+6.5+9.5}{4}=5$��$\sum_{j=1}^4{{x_j}{y_j}}=9��0.5+7��3.5+3��6.5+1��9.5=58$��$\sum_{j=1}^4{{x_j}^2}={9^2}+{7^2}+{3^2}+{1^2}=140$��
����$b=\frac{58-4��5��5}{{140-4��{5^2}}}=-\frac{21}{20}$��$a=5-��-\frac{21}{20}����5=\frac{41}{4}$��
����y����x�Ļع鷽����$y=-\frac{21}{20}x+\frac{41}{4}$��
��2���ɱ�3֪AQI������200��Ƶ��Ϊ0.1��AQIָ����200��400��Ƶ��Ϊ0.2��AQIָ������400��Ƶ��Ϊ0.7��
�衰ϴ����ÿ�����Լ200Ԫ��Ϊ�¼�A����ϴ����ÿ������Լ400Ԫ��Ϊ�¼�B����ϴ����ÿ������Լ700Ԫ��Ϊ�¼�C��
��P��A��=0.1��P��B��=0.2��P��C��=0.7��
��������ϴ����ÿ������ΪXԪ����X�ķֲ���Ϊ
| X | -200 | 400 | 700 |
| P | 0.1 | 0.2 | 0.7 |
���� ���⿼�����Իع鷽�̣�������ɢ����������ķֲ�������ѧ����������ѧ���ļ�������������ѧ�������������������������е��⣮


 �����Ļ���������人������ϵ�д�
�����Ļ���������人������ϵ�д� ���������ּ���ÿһ��ȫ�º�����ҵ��ϵ�д�
���������ּ���ÿһ��ȫ�º�����ҵ��ϵ�д� ��ٽ������½������������ϵ�д�
��ٽ������½������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����֪������S-ABCD�У�����ABCD�DZ߳�Ϊ2�����Σ���ABC=60�㣬����SADΪ�������Σ�����SAD�͵���ABCD��EΪ�߶�AD���е㣮
��ͼ����֪������S-ABCD�У�����ABCD�DZ߳�Ϊ2�����Σ���ABC=60�㣬����SADΪ�������Σ�����SAD�͵���ABCD��EΪ�߶�AD���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
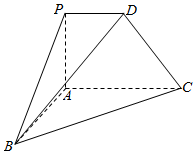 ��ͼ��������P-ABCD�У�PA��BC��ƽ��PACDΪֱ�����Σ���PAC=90�㣬PD��AC��PA=AB=PD=1��AC=2����BAC=120��
��ͼ��������P-ABCD�У�PA��BC��ƽ��PACDΪֱ�����Σ���PAC=90�㣬PD��AC��PA=AB=PD=1��AC=2����BAC=120���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | c��b��a | B�� | a��b��c | C�� | a��c��b | D�� | b��a��c |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-�ޣ�-1] | B�� | [-1��+�ޣ� | C�� | ��-�ޣ�1] | D�� | [1��+�ޣ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{2}{35}$ | B�� | $\frac{8}{35}$ | C�� | $\frac{12}{35}$ | D�� | $\frac{18}{35}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com