
| A. | c<b<a | B. | a<b<c | C. | a<c<b | D. | b<a<c |
分析 先确定三个函数在定义域上是增函数,再利用零点存在定理,求出三个函数零点的范围,从而比较大小,即可得解.
解答 解:由于:f(x)=2x+x-2,g(x)=3x+x-2,h(x)=lnx+x-2在定义域上是增函数,
对于f(x)=2x+x-2,
由于:f($\frac{1}{2}$)=$\sqrt{2}$+$\frac{1}{2}$-2<0,f(1)=2+1-2=1>0,
所以:函数在($\frac{1}{2}$,1)上有唯一的零点,即a∈($\frac{1}{2}$,1);
对于g(x)=3x+x-2,
由于:g($\frac{1}{2}$)=$\sqrt{3}$+$\frac{1}{2}$-2>0,g(0)=1+0-2=-1<0,
所以:函数在(0,$\frac{1}{2}$)上有唯一的零点,即b∈(0,$\frac{1}{2}$);
对于h(x)=lnx+x-2,
由于:h(1)=ln1+1-2=-1<0,h(2)=ln2>0,
可得:函数在(1,2)上有唯一的零点,即c∈(1,2);
则b<a<c,
故选:D.
点评 本题主要考查函数零点的大小判断,解题时注意注意函数的零点的灵活运用,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 单价x(元) | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
| 销量y(件) | 92 | 82 | 83 | 80 | 75 | 68 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,网格纸上正方形小格的边长为1(表示1cm),图中粗线画出的是一几何体的三视图,则该几何体的表面积为( )
如图,网格纸上正方形小格的边长为1(表示1cm),图中粗线画出的是一几何体的三视图,则该几何体的表面积为( )| A. | 64+24πcm2 | B. | 64+36πcm2 | C. | 48+36πcm2 | D. | 48+24πcm2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| AQI | 0~50 | 51~100 | 101~150 | 151~200 | 201~300 | >300 |
| 级别 | Ⅰ级 | Ⅱ级 | Ⅲ级 | Ⅳ级 | Ⅴ级 | Ⅵ级 |
| 类别 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
| AQI指数 | 900 | 700 | 300 | 100 |
| 空气可见度 (千米) | 0.5 | 3.5 | 6.5 | 9.5 |
| AQI指数 | [0,200] | (201,400] | (401,600] | (601,800] | (801,1000] |
| 频数 | 3 | 6 | 12 | 6 | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
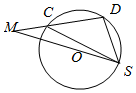 如图所示,从圆O外一点M做圆O的割线MAB、MCD,AB是圆O的直径,MA=$\sqrt{2}$,MC=$\sqrt{7}$-1,CD=2.
如图所示,从圆O外一点M做圆O的割线MAB、MCD,AB是圆O的直径,MA=$\sqrt{2}$,MC=$\sqrt{7}$-1,CD=2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com