
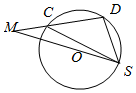
 如图所示,从圆O外一点M做圆O的割线MAB、MCD,AB是圆O的直径,MA=$\sqrt{2}$,MC=$\sqrt{7}$-1,CD=2.
如图所示,从圆O外一点M做圆O的割线MAB、MCD,AB是圆O的直径,MA=$\sqrt{2}$,MC=$\sqrt{7}$-1,CD=2.分析 (1)设圆O的半径为R,由图求出MB、MD,根据切割线定理的推论列出方程求出R;
(2)连接OC、OD,由勾股定理的逆定理判断出∠COD=90°,由圆周角与圆心角的关系求出∠CBD.
解答 解:(1)设圆O的半径为R,
因为MA=$\sqrt{2}$,MC=$\sqrt{7}-1$,CD=2,
则MB=MA+AB=$\sqrt{2}$+2R,MD=MC+CD=$\sqrt{7}+1$ (1分)
根据切割线定理的推论得:MC•MD=MA•MB (3分)
即($\sqrt{7}-1$)($\sqrt{7}+1$)=$\sqrt{2}$($\sqrt{2}$+2R)
解得:R=$\sqrt{2}$,即圆O的半径为$\sqrt{2}$ (5分)
(2)连接OC、OD,则OC=OD=$\sqrt{2}$ (6分)
$O{C}^{2}+O{D}^{2}=(\sqrt{2})^{2}+(\sqrt{2})^{2}$=4=CD2 (8分)
根据勾股定理的逆定理得,∠COD=90° (9分)
所以$∠CBD=\frac{1}{2}∠COD=45$° (10分)
点评 本题考查了切割线定理的推论,勾股定理的逆定理,以及圆周角与圆心角的关系,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | c<b<a | B. | a<b<c | C. | a<c<b | D. | b<a<c |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 平均气温x(℃) | 9 | 11 | 12 | 10 | 8 |
| 销量y(杯) | 23 | 26 | 30 | 25 | 21 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①③ | B. | ④⑤ | C. | ②④⑤ | D. | ②③④⑤ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com