
| 平均气温x(℃) | 9 | 11 | 12 | 10 | 8 |
| 销量y(杯) | 23 | 26 | 30 | 25 | 21 |
分析 (Ⅰ)根据所给的数据,先做出x,y的平均数,即做出本组数据的样本中心点,根据最小二乘法求出线性回归方程的系数,写出线性回归方程.
(Ⅱ)利用线性回归方程,x取20,即可预测平均气温约为20℃时该奶茶店的这种饮料销量.
解答 解:(Ⅰ)$\overline{x}$=10,$\overline{y}$=25--------------(1分)
b=$\frac{1271-5×10×25}{510-5×100}$=2.1--------------(2分)
a=25-2.1×10=4--------------(4分)
y关于x的线性回归方程$\widehat{y}$=2.1x+4--------------(8分)
(Ⅱ)当x=20时,y=42+4=46.
故预测平均气温约为20°C时该奶茶店的这种饮料销量为46杯--------------(12分)
点评 本题考查线性回归方程的求法,考查最小二乘法,考查估计验算所求的方程是否是可靠的,是一个基础题.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
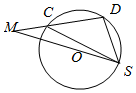 如图所示,从圆O外一点M做圆O的割线MAB、MCD,AB是圆O的直径,MA=$\sqrt{2}$,MC=$\sqrt{7}$-1,CD=2.
如图所示,从圆O外一点M做圆O的割线MAB、MCD,AB是圆O的直径,MA=$\sqrt{2}$,MC=$\sqrt{7}$-1,CD=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | 1 | 2 | 3 | 4 |
| y | 3 | 3 | 5 | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | c>a>b | B. | a>c>b | C. | a>b>c | D. | b>a>c |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 记忆能力x | 4 | 6 | 8 | 10 |
| 识图能力y | 3 | 5 | 6 | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
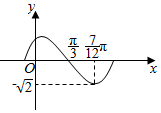 函数f(x)=Asin(ωx+φ)(A>0,ω>0)的部分图象如图所示,则f($\frac{π}{4}$)=$\frac{\sqrt{2}}{2}$.π
函数f(x)=Asin(ωx+φ)(A>0,ω>0)的部分图象如图所示,则f($\frac{π}{4}$)=$\frac{\sqrt{2}}{2}$.π查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com