
分析 (1)求出函数的导数,解关于导函数的不等式求出函数 的极小值,结合函数的单调性求出函数的零点个数即可;
(2)求出F(x)的导数,分离参数得到2a≥lnx-3x2+1恒成立,设h(x)=lnx-3x2+1,h′(x)=$\frac{1}{x}$-6x,根据函数的单调性求出h(x)的最大值,从而求出a的范围即可.
解答 解:(1)f(x)=xlnx-ax,定义域是(0,+∞),
f′(x)=lnx+1-a=0,
令f′(x)>0,解得:x>ea-1,
令f′(x)<0,解得:0<x<ea-1,
∴f(x)在(0,ea-1)递减,在(ea-1,+∞)递增,
∴f(x)极小值=f(ea-1),无极大值,
∵f(ea-1)=-ea-1<0,x→0时,f(x)→0,
∴f(x)=0在(0,+∞)上仅有一个实数根;
(2)由F(x)=f(x)-g(x)=xlnx-2ax-x3-a在(0,+∞)递减,
得:F′(x)=lnx+1-2a-3x2≤0在(0,+∞)恒成立,
即:2a≥lnx-3x2+1恒成立,
设h(x)=lnx-3x2+1,h′(x)=$\frac{1}{x}$-6x,
令h′(x)>0,解得:0<x<$\frac{\sqrt{6}}{6}$,令h′(x)<0,解得:x>$\frac{\sqrt{6}}{6}$,
∴h(x)在(0,$\frac{\sqrt{6}}{6}$)递增,在($\frac{\sqrt{6}}{6}$,+∞)递减,
∴h(x)最大值=h($\frac{\sqrt{6}}{6}$)=$\frac{1}{2}$(1-ln6),
∴a≥$\frac{1}{4}$(1-ln6).
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及函数的零点问题,是一道中档题.


科目:高中数学 来源: 题型:选择题
| A. | $f(1)>\frac{f(0)}{{\sqrt{e}}}$ | B. | $f(2)<\frac{f(0)}{e}$ | C. | $f(1)>\sqrt{e}f(2)$ | D. | f(0)>e2f(4) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 单价x(元) | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
| 销量y(件) | 92 | 82 | 83 | 80 | 75 | 68 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| AQI | 0~50 | 51~100 | 101~150 | 151~200 | 201~300 | >300 |
| 级别 | Ⅰ级 | Ⅱ级 | Ⅲ级 | Ⅳ级 | Ⅴ级 | Ⅵ级 |
| 类别 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
| AQI指数 | 900 | 700 | 300 | 100 |
| 空气可见度 (千米) | 0.5 | 3.5 | 6.5 | 9.5 |
| AQI指数 | [0,200] | (201,400] | (401,600] | (601,800] | (801,1000] |
| 频数 | 3 | 6 | 12 | 6 | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\widehat{y}$=x-1 | B. | $\widehat{y}$=2x+1 | C. | $\widehat{y}$=x+2 | D. | $\widehat{y}$=x+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
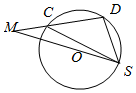 如图所示,从圆O外一点M做圆O的割线MAB、MCD,AB是圆O的直径,MA=$\sqrt{2}$,MC=$\sqrt{7}$-1,CD=2.
如图所示,从圆O外一点M做圆O的割线MAB、MCD,AB是圆O的直径,MA=$\sqrt{2}$,MC=$\sqrt{7}$-1,CD=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | c>a>b | B. | a>c>b | C. | a>b>c | D. | b>a>c |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5.2 | B. | 6.6 | C. | 7.1 | D. | 8.3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com