
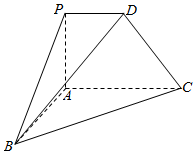
 如图,在四棱锥P-ABCD中,PA⊥BC,平面PACD为直角梯形,∠PAC=90°,PD∥AC,PA=AB=PD=1,AC=2,∠BAC=120°
如图,在四棱锥P-ABCD中,PA⊥BC,平面PACD为直角梯形,∠PAC=90°,PD∥AC,PA=AB=PD=1,AC=2,∠BAC=120°分析 (Ⅰ)由PA⊥BC,PA⊥AC,得到PA⊥平面ABC,由此能证明PA⊥AB.
(Ⅱ)过点B作BM⊥CA交CA延长线于点M,连结DM,则∠BDM即是直线BD与平面PACD所成角,由此能求出直线BD与平面PACD所成角的正弦值.
(Ⅲ)过点E作EF⊥BC,垂足为F,连接DF,则∠DFE为二面角D-BC-A的平面角,由此能求出二面角D-BC-A的平面角的正切值.
解答 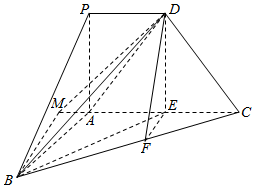 (本小题满分13分)
(本小题满分13分)
证明:(Ⅰ)因为PA⊥BC,∠PAC=90°,
即PA⊥AC,因为AC,BC交于点C,
所以PA⊥平面ABC,…(2分)
而AB?底面ABC,所以PA⊥AB.…(3分)
解:(Ⅱ)由(Ⅰ)可知,平面PACD⊥平面ABC,
过点B作BM⊥CA交CA延长线于点M,连结DM,
则∠BDM即是直线BD与平面PACD所成角;…(5分)
取AC的中点E,连接BE,DE,则DE∥PA;
在△ABE中,AB=AE=1,∠BAE=120°,
所以BE=$\sqrt{{1}^{2}+{1}^{2}-2×1×1×cos120°}$=$\sqrt{3}$,$AM=\frac{1}{2}AB=\frac{1}{2}$,
所以$BM=\frac{{\sqrt{3}}}{2}$…(6分)
因为DE∥PA,所以DE⊥平面ABC,BD=$\sqrt{3+1}$=2,…(7分)
在直角三角形△BDM中,$sin∠BDM=\frac{BM}{BD}=\frac{{\sqrt{3}}}{4}$,
即直线BD与平面PACD所成角的正弦值为$\frac{{\sqrt{3}}}{4}$.…(8分)
(Ⅲ)过点E作EF⊥BC,垂足为F,连接DF,
则∠DFE为二面角D-BC-A的平面角,…(10分)
在△EBC中,$BE=\sqrt{3},EC=1,∠BEC={150°}$,
则BC=$\sqrt{3+1-2×\sqrt{3}×1×cos150°}$=$\sqrt{7}$,
${S_{△EBC}}=\frac{1}{2}BE•ECsin∠BEC=\frac{1}{2}BC•EF$,$EF=\frac{{\sqrt{21}}}{14}$,…(11分)
$tan∠DFE=\frac{DE}{EF}=\frac{{2\sqrt{21}}}{3}$,
即二面角D-BC-A的平面角的正切值为$\frac{{2\sqrt{21}}}{3}$.…(13分)
点评 本题考查异面直线垂直的证明,考查线面角的正弦值的求法,考查二面角的正切值的求法,解题时要认真审题,注意空间思维能力的培养.


科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | $\frac{19}{4}$ | C. | $\frac{9}{2}$ | D. | $\frac{25}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
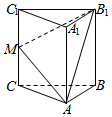 如图,在三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AC=BC=2,AB=2$\sqrt{2}$,CC1=4,M是棱CC1上一点.
如图,在三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AC=BC=2,AB=2$\sqrt{2}$,CC1=4,M是棱CC1上一点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 单价x(元) | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
| 销量y(件) | 92 | 82 | 83 | 80 | 75 | 68 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在某产品表面进行腐蚀刻度线实验,得到腐蚀深度y与腐蚀时间x之间相应的一组观察值如表:
在某产品表面进行腐蚀刻度线实验,得到腐蚀深度y与腐蚀时间x之间相应的一组观察值如表:| x(s) | 5 | 10 | 15 | 20 | 30 | 40 | 50 | 60 | 70 | 90 | 120 |
| y(μm) | 6 | 10 | 10 | 13 | 16 | 17 | 19 | 23 | 25 | 29 | 46 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| AQI | 0~50 | 51~100 | 101~150 | 151~200 | 201~300 | >300 |
| 级别 | Ⅰ级 | Ⅱ级 | Ⅲ级 | Ⅳ级 | Ⅴ级 | Ⅵ级 |
| 类别 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
| AQI指数 | 900 | 700 | 300 | 100 |
| 空气可见度 (千米) | 0.5 | 3.5 | 6.5 | 9.5 |
| AQI指数 | [0,200] | (201,400] | (401,600] | (601,800] | (801,1000] |
| 频数 | 3 | 6 | 12 | 6 | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\widehat{y}$=x-1 | B. | $\widehat{y}$=2x+1 | C. | $\widehat{y}$=x+2 | D. | $\widehat{y}$=x+1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com