
����Ŀ��ijУ�߶���1����ѧ��Ϊ�˳�뾭�Ѹ����Ϲ����������ί�������һ�����ʵ��С�飬����������ٰ��·ݣ�30����㣩��������ȥ����һ��ʱ��ˮ��.����30����ÿ��ˮ��������![]() ��Ԫ����ʱ��
��Ԫ����ʱ��![]() ���죩�IJ����������±���ʾ����֪������
���죩�IJ����������±���ʾ����֪������![]() �����ʱ��
�����ʱ��![]() ���죩����һ�κ�����ϵ.
���죩����һ�κ�����ϵ.
��1�������ṩ��ͼ��ͱ����³�ÿ��ˮ��������![]() ��Ԫ����ʱ��
��Ԫ����ʱ��![]() ���죩������ĺ�����ϵʽ����������
���죩������ĺ�����ϵʽ����������![]() �����ʱ��
�����ʱ��![]() ���죩��һ�κ�����ϵ��
���죩��һ�κ�����ϵ��
��2����![]() ��Ԫ����ʾ����ˮ���������룬д��
��Ԫ����ʾ����ˮ���������룬д��![]() ��
��![]() �ĺ�����ϵʽ��������30���еڼ���������������ֵΪ����Ԫ��
�ĺ�����ϵʽ��������30���еڼ���������������ֵΪ����Ԫ��

���𰸡���1����������2���ڵ�ʮ��ʱ������������ֵΪ90Ԫ.
�������������������1������![]() �����߶�
�����߶�![]() ����
����![]() ��
�� ![]() ��
��![]() ����ֵ�����߶�
����ֵ�����߶�![]() ����
����![]() ��
�� ![]() ��
��![]() ��ֵ���Ӷ��ɵý������2�����������ˮ����������ĺ�����ϵʽ
��ֵ���Ӷ��ɵý������2�����������ˮ����������ĺ�����ϵʽ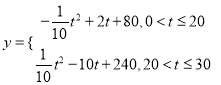 �����ö��κ����ֱ��жϳ������κ����ĵ����ԣ����õ����Էֱ�������ֵ���ٱȽϴ�С����.
�����ö��κ����ֱ��жϳ������κ����ĵ����ԣ����õ����Էֱ�������ֵ���ٱȽϴ�С����.
�����������1�����������![]() ����
����![]() ʱ���߶�
ʱ���߶�![]() ����
����![]() ��
�� ![]() ��
��![]() ��
��
��![]() ʱ���߶�
ʱ���߶�![]() ����
����![]() ��
�� ![]() ��
��![]() .
.
����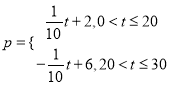 .
.
��![]() ���ɱ������ݵ�
���ɱ������ݵ�![]() ������
������![]() .
.
��2����![]() ��
��
��![]() ʱ��
ʱ�� ![]() ��
��![]() �ϵĵ�����������
�ϵĵ�����������![]() �ϵ����ݼ������Ե�
�ϵ����ݼ������Ե�![]() ʱ��
ʱ�� ![]() �����ֵΪ
�����ֵΪ![]() Ԫ����
Ԫ����![]() ʱ��
ʱ�� ![]() ��
��![]() �ϵ����ݼ�������
�ϵ����ݼ�������![]() .
.
�ۺ������ã��ڵ�ʮ��ʱ������������ֵΪ90Ԫ.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������f��x��=ax2+2��a��3��x+1������[��2��+�ޣ��ϵݼ�����ʵ��a��ȡֵ��Χ�ǣ� ��
A.�����ޣ���3]
B.[��3��0]
C.[��3��0��
D.[��2��0]
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ҹ��Ŵ���ѧ�����������������С����н�����ߣ�ն��һ�ߣ����Ľնĩһ�ߣ��ض���ʴ�һ�߸��ؼ��Σ�����˼�ǣ�������һ����һͷ�֣�һͷϸ���ڴֵ�һ�˽���1�ߣ���4���ϸ��һ�˽���1�ߣ���2�������ÿһ�߸��ض��ٽ�������������֪�����������ɴֵ�ϸ�����ε�����С�ģ������м�һ�ߵ�����Ϊ________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������6ֻ���ݣ�������2ֻ�Ǵ�Ʒ��4ֻ����Ʒ��������ȡ2ֻ�����������¼��ĸ��ʣ�
����ȡ����2ֻ���Ǵ�Ʒ��
����ȡ����2ֻ��ǡ��һֻ��Ʒ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() ��
�� ![]() �ֱ�Ϊ�Ȳ����к͵ȱ����У�
�ֱ�Ϊ�Ȳ����к͵ȱ����У� ![]() ��
�� ![]() ��ǰ
��ǰ![]() ���Ϊ
���Ϊ![]() .����
.����![]() �ĵ�������
�ĵ�������![]() ����
����![]() ����
����![]() �Ǻ���
�Ǻ���![]() �����.
�����.
��1����![]() ��ֵ��
��ֵ��
��2��������![]() ����Ϊ
����Ϊ![]() ���ҵ�
���ҵ�![]() ����
����![]() ʱ���е㶼��ָ������
ʱ���е㶼��ָ������![]() ��ͼ����.
��ͼ����.
�������![]() ����ʽ����֤����
����ʽ����֤���� ![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ��ˮ�¿��Ż�У�ijһDZˮԱ��DZˮ50��ˮ���п�����ҵ�������������������������棺
����DZƽ���ٶ�Ϊ![]() ��/���ӣ�ÿ���ӵ�������Ϊ
��/���ӣ�ÿ���ӵ�������Ϊ![]() ����
����
��ˮ����ҵʱ�䷶Χ������10�������20���ӣ�ÿ����������Ϊ0.3����
�۷���ˮ��ʱ��ƽ���ٶ�Ϊ![]() ��/���ӣ�ÿ����������Ϊ0.32����DZˮԱ�ڴ˴ο��Ż�е���������Ϊ
��/���ӣ�ÿ����������Ϊ0.32����DZˮԱ�ڴ˴ο��Ż�е���������Ϊ![]() ��.
��.
��1�����ˮ����ҵʱ����10���ӣ���![]() ��ʾΪ
��ʾΪ![]() �ĺ�����
�����
��2����![]() ��ˮ����ҵʱ��Ϊ20���ӣ�����������
��ˮ����ҵʱ��Ϊ20���ӣ�����������![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��3����DZˮԱЯ������13.5��������DZˮԱ�����ˮ�¶��ٷ��ӣ����ȡ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() ��
�� ![]() ����Բ
����Բ![]() ��
��![]() �ij���Ϊ���ᣬ����
�ij���Ϊ���ᣬ����![]() ����ͬ��������.
����ͬ��������.
��1������Բ![]() �ķ��̣�
�ķ��̣�
��2����![]() Ϊ����ԭ�㣬��
Ϊ����ԭ�㣬��![]() �ֱ�����Բ
�ֱ�����Բ![]() ��
��![]() �ϣ�
�ϣ� ![]() ����ֱ��
����ֱ��![]() �ķ���.
�ķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ ![]() �Ƕ����ڣ����ޣ�+�ޣ��ϵ��溯����������
�Ƕ����ڣ����ޣ�+�ޣ��ϵ��溯���������� ![]()
��1����ʵ��a��b����ȷ������f��x���Ľ���ʽ
��2���ö���֤��f��x���ڣ���1��1��������������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com