
解答题:要求写出文字说明、证明过程和演算步骤
在三棱锥S-ABC中,侧面SAC⊥底面ABC,△SAC是边长为4的正三角形,△ACB为直角三角形,∠ACB=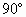 ,BC=4
,BC=4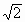 .
.

(Ⅰ)求证:侧面SAC⊥侧面BSC;
(Ⅱ)求SB与底面ABC所成角;
(Ⅲ)求二面角S—AB—C的正切值.
|
(1)证明:∵∠ACB= 又面SAC⊥面ABC,面SAC∩面ABC=AC ∴BC⊥面SAC 又BCÌ 面SBC ∴面SAC⊥面BSC (2)解:取AC的中点D,连SD、BD ∵△SAC为正三角形,边长为4 ∴SD⊥AC且SD=2 又 面SAC⊥面ABC ∴SD⊥面ABC ∴∠SBD为SB与面ABC所成角 在Rt△BCD中,∠BCA=Rt∠,BC=4 ∴BD=6 在Rt△SBD中,SD=2 ∴∠SBD= (3)解:过D作DE⊥AB于E,连SE则SE⊥AB ∠SED为S-AB-C的平面角 在△ABC与△ADE中 AB=4 ∴ ∴ ∴tan∠SED |


科目:高中数学 来源:2002年全国各省市高考模拟试题汇编 题型:044
解答题:要求写出文字说明、证明过程和演算步骤
数列{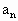 }是由正数组成的等比数列,数列{
}是由正数组成的等比数列,数列{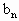 }满足:
}满足:
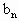 =
=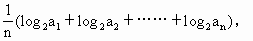
(Ⅰ)记数列{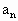 }的公比为q,若数列{
}的公比为q,若数列{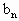 }的前n项和存在最大值,求q的取值范围;
}的前n项和存在最大值,求q的取值范围;
(Ⅱ)若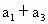 =20,
=20,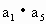 =16,从数列{
=16,从数列{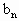 }中依次取出第2项,第4项,第8项,……第
}中依次取出第2项,第4项,第8项,……第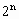 项,……,组成数列{
项,……,组成数列{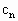 },求数列{
},求数列{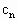 }的前n项和.
}的前n项和.
查看答案和解析>>
科目:高中数学 来源:2002年全国各省市高考模拟试题汇编 题型:044
解答题:要求写出文字说明、证明过程和演算步骤
已知椭圆C的方程为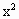 +
+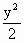 =1,点P(
=1,点P(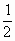 ,1)是椭圆内的定点,过点P的直线l与椭圆C交于A、B两点,点Q为线段AB的中点,求
,1)是椭圆内的定点,过点P的直线l与椭圆C交于A、B两点,点Q为线段AB的中点,求
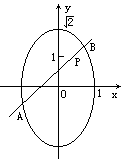
(Ⅰ)点Q的轨迹方程;
(Ⅱ)点Q的轨迹与坐标轴的交点为顶点的多边形的外接圆方程.
查看答案和解析>>
科目:高中数学 来源:哈尔滨市第三中学2006-2007学年度高三年级上学期月考、数学试题(理) 题型:044
| |||||||||||
查看答案和解析>>
科目:高中数学 来源:山东省蓬莱、牟平2006—2007学年度第一学期高三年级期中考试、数学试题(文科) 题型:044
解答题:解答时要求写出必要的文字说明或推演步骤.
已知![]() =(1,x),
=(1,x),![]() =(x2+x,-x),m为实数,求使
=(x2+x,-x),m为实数,求使![]() 成立的x的范围.
成立的x的范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com