
| A. | 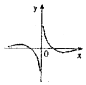 | B. | 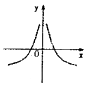 | C. | 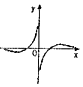 | D. | 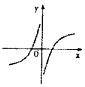 |
分析 利用指数函数的性质求出a的范围,判断函数的奇偶性排除选项,利用特殊值判断即可.
解答 解:当x∈R时,函数f(x)=a|x|(a>0且a≠0)始终满足f(x)≥1,
可得a>1,
则函数$y=\frac{{{{log}_a}|x|}}{x^3}$是奇函数,可知B不正确;
当x→0+,时,函数$y=\frac{{{{log}_a}|x|}}{x^3}$<0,排除A,
当x=a10时,函数$y=\frac{{{{log}_a}|x|}}{x^3}$=$\frac{10}{{a}^{30}}$→0,排除D,
故选:C.
点评 本题考查函数的图象的判断与应用,注意函数的奇偶性,指数函数的性质,特殊值的判断与应用.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
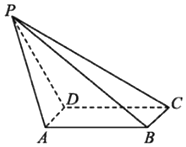 如图,在四棱锥P-ABCD中,底面ABCD是矩形,AD⊥PD,BC=1,PC=2$\sqrt{3}$,PD=CD=2,则二面角A-PB-C的正切值为$\frac{\sqrt{15}}{9}$.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,AD⊥PD,BC=1,PC=2$\sqrt{3}$,PD=CD=2,则二面角A-PB-C的正切值为$\frac{\sqrt{15}}{9}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
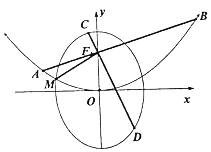 已知F1为椭圆C1:$\frac{{y}^{2}}{{a}^{2}}+\frac{{x}^{2}}{{b}^{2}}$=1的上焦点,F1也是抛物线C2:x2=4y的焦点,点M是C1与C2在第二象限的交点,且|MF1|=$\frac{5}{3}$.
已知F1为椭圆C1:$\frac{{y}^{2}}{{a}^{2}}+\frac{{x}^{2}}{{b}^{2}}$=1的上焦点,F1也是抛物线C2:x2=4y的焦点,点M是C1与C2在第二象限的交点,且|MF1|=$\frac{5}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

| $\overline x$ | $\overline y$ | $\overline w$ | ${\sum_{i=1}^8{({x_i}-\overline x)}^2}$ | ${\sum_{i=1}^8{({w_i}-\overline w)}^2}$ | $\sum_{i=1}^8{({x_i}-\overline x)}({y_i}-\overline y)$ | $\sum_{i=1}^8{({w_i}-\overline w)}({y_i}-\overline y)$ |
| 46.6 | 56.3 | 6.8 | 289.8 | 1.6 | 1469 | 108.8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com