
【题目】已知函数![]() .
.
(1)关于![]() 的不等式
的不等式![]() 的解集为
的解集为![]() ,求
,求![]() 的值;
的值;
(2)若函数![]() 的图象与
的图象与![]() 轴围成图形的面积不小于50,求
轴围成图形的面积不小于50,求![]() 的取值范围.
的取值范围.
【答案】(1) ![]() (2)
(2) ![]()
【解析】
(1)当![]() 时,求得不等式
时,求得不等式![]() 的解集为空集,当
的解集为空集,当![]() 时,求得函数
时,求得函数![]() 的单调性,根据不等式
的单调性,根据不等式![]() 的解集为
的解集为![]() ,列出方程组,即可求解;
,列出方程组,即可求解;
(2)由(1)知,当![]() 时不合题意;当
时不合题意;当![]() 时,
时,![]() ,当
,当![]() 时,求得函数
时,求得函数![]() 的图象与
的图象与![]() 轴的交点为
轴的交点为![]() 和
和![]() ,得到关于面积的不等式,即可求解.
,得到关于面积的不等式,即可求解.
(1)当![]() 时,
时,![]() ,则关于
,则关于![]() 的不等式
的不等式![]() 的解集为空集,不合题意,
的解集为空集,不合题意,
当![]() 时,
时,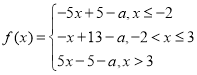 ,
,
所以函数![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增,
上单调递增,
因为关于![]() 的不等式
的不等式![]() 的解集为
的解集为![]() ,
,
所以![]() ,即
,即![]() ,解得
,解得![]() .
.
(2)设函数![]() 的图象与
的图象与![]() 轴围成图形面积为
轴围成图形面积为![]() ,
,
由(1)知,当![]() 时,
时,![]() ,不合题意;
,不合题意;
当![]() 时,
时,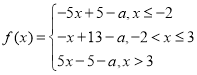 ,
,
当![]() 时,
时,![]() ,
,
当![]() 时,函数
时,函数![]() 的图象与
的图象与![]() 轴的交点为
轴的交点为![]() 和
和![]() ,
,
此时函数![]() 的图象与
的图象与![]() 轴围成图形面积为
轴围成图形面积为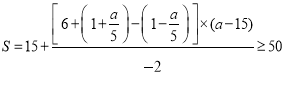 ,
,
化简得![]() ,解得
,解得![]() 或
或![]() (舍去),
(舍去),
所以实数![]() 的取值范围是
的取值范围是![]() .
.


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 1(a>b>0),椭圆C上的点到焦点距离的最大值为9,最小值为1.
1(a>b>0),椭圆C上的点到焦点距离的最大值为9,最小值为1.
(1)求椭圆C的标准方程;
(2)求椭圆C上的点到直线l:4x﹣5y+40=0的最小距离?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列1,1,2,1,2,4,1,2,4,8,1,2,4,8,16,![]() 其中第一项是
其中第一项是![]() ,接下来的两项是
,接下来的两项是![]() ,
,![]() ,再接下来的三项是
,再接下来的三项是![]() ,
,![]() ,
,![]() ,依此类推那么该数列的前50项和为
,依此类推那么该数列的前50项和为![]()
![]()
A. 1044 B. 1024 C. 1045 D. 1025
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设圆![]() 的圆心为
的圆心为![]() ,直线
,直线![]() 过点
过点![]() 且与
且与![]() 轴不重合,交圆
轴不重合,交圆![]() 于
于![]() ,
,![]() 两点,过点
两点,过点![]() 作
作![]() 的平行线交
的平行线交![]() 于点
于点![]() .
.
(1)求![]() 的值;
的值;
(2)设点![]() 的轨迹为曲线
的轨迹为曲线![]() ,直线
,直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,与直线
两点,与直线![]() 相交于
相交于![]() 点,试问在椭圆
点,试问在椭圆![]() 上是否存在一定点
上是否存在一定点![]() ,使得
,使得![]() ,
,![]() ,
,![]() 成等差数列(其中
成等差数列(其中![]() ,
,![]() ,
,![]() 分别指直线
分别指直线![]() ,
,![]() ,
,![]() 的斜率).若存在,求出
的斜率).若存在,求出![]() 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,四边形ABCD是菱形,![]() ,BD=2.
,BD=2.
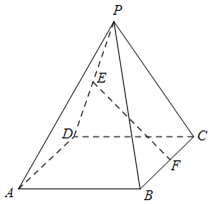
(1)若点E,F分别为线段PD,BC上的中点,求证:EF∥平面PAB;
(2)若平面PBD⊥平面ABCD,且PD⊥PB,PD=PB,求平面PAB与平面PBC所成的锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,2012年春节,摄影爱好者S在某公园A处,发现正前方B处有一立柱,测得立柱顶端O的仰角和立柱底部B的俯角均为![]() ,已知S的身高约为
,已知S的身高约为![]() 米(将眼睛距地面的距离按
米(将眼睛距地面的距离按![]() 米处理)
米处理)
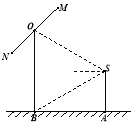
(1) 求摄影者到立柱的水平距离和立柱的高度;
(2) 立柱的顶端有一长2米的彩杆MN绕中点O在S与立柱所在的平面内旋转.摄影者有一视角范围为![]() 的镜头,在彩杆转动的任意时刻,摄影者是否都可以将彩杆全部摄入画面?说明理由.
的镜头,在彩杆转动的任意时刻,摄影者是否都可以将彩杆全部摄入画面?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A为焦距为![]() 的椭圆E:
的椭圆E:![]() (a>b>0)的右顶点,点P(0,
(a>b>0)的右顶点,点P(0,![]() ),直线PA交椭圆E于点B,
),直线PA交椭圆E于点B,![]() .
.
(1)求椭圆E的方程;
(2)设过点P且斜率为![]() 的直线
的直线![]() 与椭圆E交于M、N两点(M在P、N之间),若四边形MNAB的面积是△PMB面积的5倍.求直线
与椭圆E交于M、N两点(M在P、N之间),若四边形MNAB的面积是△PMB面积的5倍.求直线![]() 的斜率
的斜率![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AB是圆O的直径,点C是圆O上异于A,B的点,直线PC⊥平面ABC,E,F分别是PA,PC的中点.
(1)记平面BEF与平面ABC的交线为l,试判断直线l与平面PAC的位置关系,并加以证明;
(2)设(1)中的直线l与圆O的另一个交点为D,且点Q满足![]() .记直线PQ与平面ABC所成的角为θ,异面直线PQ与EF所成的角为α,二面角E﹣l﹣C的大小为β.求证:sinθ=sinαsinβ.
.记直线PQ与平面ABC所成的角为θ,异面直线PQ与EF所成的角为α,二面角E﹣l﹣C的大小为β.求证:sinθ=sinαsinβ.
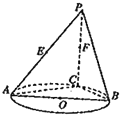
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com