
【题目】已知A为焦距为![]() 的椭圆E:
的椭圆E:![]() (a>b>0)的右顶点,点P(0,
(a>b>0)的右顶点,点P(0,![]() ),直线PA交椭圆E于点B,
),直线PA交椭圆E于点B,![]() .
.
(1)求椭圆E的方程;
(2)设过点P且斜率为![]() 的直线
的直线![]() 与椭圆E交于M、N两点(M在P、N之间),若四边形MNAB的面积是△PMB面积的5倍.求直线
与椭圆E交于M、N两点(M在P、N之间),若四边形MNAB的面积是△PMB面积的5倍.求直线![]() 的斜率
的斜率![]() .
.
【答案】(1)![]() +
+![]() =1;(2)k=±
=1;(2)k=±![]()
【解析】
(1)先根据条件得B点坐标,代入椭圆方程,再与焦距联立方程组解得![]() (2)根据面积关系得
(2)根据面积关系得![]() ,联立直线方程与椭圆方程,利用韦达定理建立等量关系解得斜率.
,联立直线方程与椭圆方程,利用韦达定理建立等量关系解得斜率.
(1)由题意,得焦距2c=2![]() ,∴2c=2
,∴2c=2![]() ,c=
,c=![]() ,
,
∵![]() ,所以点B为线段AP的中点,
,所以点B为线段AP的中点,
因为点P(0,2![]() ),A(a,0),
),A(a,0),
∴B(![]() ,
,![]() ),
),
因为点B(![]() ,
,![]() )在椭圆E上,∴
)在椭圆E上,∴![]() +
+![]() =1,
=1,
即b2=4,![]() 2=b2+c2=9,
2=b2+c2=9,
∴椭圆E的方程为![]() +
+![]() =1.
=1.
(2)由题可得S△PAN=6S△PBM,即![]() |PA||PN|sin∠APN=6×
|PA||PN|sin∠APN=6×![]() |PB||PM|sin∠BPM,
|PB||PM|sin∠BPM,
∴|PN|=3|![]() |,∴
|,∴![]() ,设M(x1,y1),N(x2,y2),
,设M(x1,y1),N(x2,y2),
于是![]() =(x1,y1-2
=(x1,y1-2![]() ),
),![]() =(x2,y2-2
=(x2,y2-2![]() ),
),
∴3(x1,y1-2![]() )=(x2,y2-2
)=(x2,y2-2![]() ),
),
∴x2=3 x1,即![]() =3,于是
=3,于是![]() +
+![]() =
=![]() ,即
,即![]() =
=![]() ,①,
,①,
联立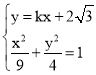 ,消去y,整理得(9k2+4)x2+36
,消去y,整理得(9k2+4)x2+36![]() kx+72=0,
kx+72=0,
由△=(36![]() k)2-4×(9k2+4)×72>0,解得k2>
k)2-4×(9k2+4)×72>0,解得k2>![]() ,
,
∴x1+x2=-![]() ,x1x2=
,x1x2=![]() ,
,
代入①可解得k2=![]() ,满足k2>
,满足k2>![]() ,∴k=±
,∴k=±![]() ,即直线l的斜率k=±
,即直线l的斜率k=±![]() .
.


科目:高中数学 来源: 题型:
【题目】一个盒子里有大小相同的3个红球和3个黑球,从盒子里随机取球,取到每个球的可能性是相同的,设取到一个红球得1分,取到一个黑球得0分.
(Ⅰ)若从盒子里一次随机取出了3个球,求得2分的概率;
(Ⅱ)着从盒子里每次摸出一个球,看清颜色后放回,连续摸3次,求得分ξ的概率分布列及期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() 为参数),以
为参数),以![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,点
,点![]() 是曲线
是曲线![]() 上的动点,点
上的动点,点![]() 在
在![]() 的延长线上,且
的延长线上,且![]() ,点
,点![]() 的轨迹为
的轨迹为![]() .
.
(1)求直线![]() 及曲线
及曲线![]() 的极坐标方程;
的极坐标方程;
(2)若射线![]() 与直线
与直线![]() 交于点
交于点![]() ,与曲线
,与曲线![]() 交于点
交于点![]() (与原点不重合),求
(与原点不重合),求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是菱形,
是菱形,![]() ,
,![]() 为等边三角形,
为等边三角形,![]() 是线段
是线段![]() 上的一点,且
上的一点,且![]() 平面
平面![]() .
.

(1)求证:![]() 为
为![]() 的中点;
的中点;
(2)若![]() 为
为![]() 的中点,连接
的中点,连接![]() ,
,![]() ,
,![]() ,
,![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校学生社团组织活动丰富,学生会为了解同学对社团活动的满意程度,随机选取了100位同学进行问卷调查,并将问卷中的这100人根据其满意度评分值(百分制)按照[40,50),[50,60),[60,70),…,[90,100]分成6组,制成如图所示频率分布直方图.
(1)求图中x的值;
(2)求这组数据的中位数;
(3)现从被调查的问卷满意度评分值在[60,80)的学生中按分层抽样的方法抽取5人进行座谈了解,再从这5人中随机抽取2人作主题发言,求抽取的2人恰在同一组的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】今年入冬以来,我市天气反复.在下图中统计了我市上个月前15天的气温,以及相对去年同期的气温差(今年气温-去年气温,单位:摄氏度),以下判断错误的是( )
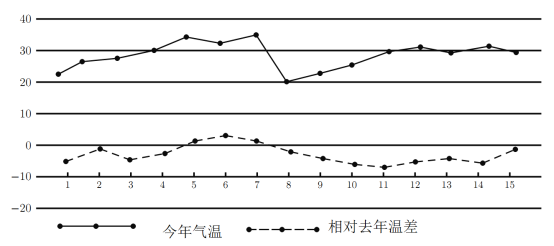
A.今年每天气温都比去年气温低B.今年的气温的平均值比去年低
C.今年8-12号气温持续上升D.今年8号气温最低
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com