
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() 为参数),以
为参数),以![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,点
,点![]() 是曲线
是曲线![]() 上的动点,点
上的动点,点![]() 在
在![]() 的延长线上,且
的延长线上,且![]() ,点
,点![]() 的轨迹为
的轨迹为![]() .
.
(1)求直线![]() 及曲线
及曲线![]() 的极坐标方程;
的极坐标方程;
(2)若射线![]() 与直线
与直线![]() 交于点
交于点![]() ,与曲线
,与曲线![]() 交于点
交于点![]() (与原点不重合),求
(与原点不重合),求![]() 的最大值.
的最大值.
科目:高中数学 来源: 题型:
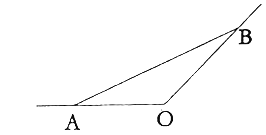
【题目】如图所示,某城市有一条从正西方AO通过市中心O后向东北OB的公路,现要修一条地铁L,在OA,OB上各设一站A,B,地铁在AB部分为直线段,现要求市中心O与AB的距离为![]() ,设地铁在AB部分的总长度为
,设地铁在AB部分的总长度为![]() .
.
![]() 按下列要求建立关系式:
按下列要求建立关系式:
![]() 设
设![]() ,将y表示成
,将y表示成![]() 的函数;
的函数;
![]() 设
设![]() ,
,![]() 用m,n表示y.
用m,n表示y.
![]() 把A,B两站分别设在公路上离中心O多远处,才能使AB最短?并求出最短距离.
把A,B两站分别设在公路上离中心O多远处,才能使AB最短?并求出最短距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】图①是一栋新农村别墅,它由上部屋顶和下部主体两部分组成.如图②,屋顶由四坡屋面构成,其中前后两坡屋面ABFE和CDEF是全等的等腰梯形,左右两坡屋面EAD和FBC是全等的三角形.点F在平面ABCD和BC上的射影分别为H,M.已知HM 5 m,BC 10 m,梯形ABFE的面积是△FBC面积的2.2倍.设∠FMH ![]()
![]() .
.
(1)求屋顶面积S关于![]() 的函数关系式;
的函数关系式;
(2)已知上部屋顶造价与屋顶面积成正比,比例系数为k(k为正的常数),下部主体造价与其 高度成正比,比例系数为16 k.现欲造一栋上、下总高度为6 m的别墅,试问:当![]() 为何值时,总造价最低?
为何值时,总造价最低?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l的参数方程为 为参数
为参数![]() ,以坐标原点为极点,x轴的正半轴为极轴建建立极坐标系,曲线C的极坐标方程为
,以坐标原点为极点,x轴的正半轴为极轴建建立极坐标系,曲线C的极坐标方程为![]() .
.
![]() 求曲线C的直角坐标方程与直线l的极坐标方程;
求曲线C的直角坐标方程与直线l的极坐标方程;
![]() Ⅱ
Ⅱ![]() 若直线
若直线![]() 与曲线C交于点
与曲线C交于点![]() 不同于原点
不同于原点![]() ,与直线l交于点B,求
,与直线l交于点B,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在![]() 上的函数
上的函数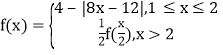 及如下的4个命题:
及如下的4个命题:
![]() 关于x的方程
关于x的方程![]() 有
有![]() 个不同的零点;
个不同的零点;
![]() 对于实数
对于实数![]() ,不等式
,不等式![]() 恒成立;
恒成立;
![]() 在
在![]() 上,方程
上,方程![]() 有5个零点;
有5个零点;
![]() 时,函数
时,函数![]() 的图象与x轴图成的形的面积是4.
的图象与x轴图成的形的面积是4.
则以上命题正确的为______![]() 把正确命题前的序号填在横线上
把正确命题前的序号填在横线上![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com