
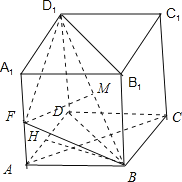
【题目】如图,已知在棱柱![]() 的面底是菱形,且
的面底是菱形,且![]() 面ABCD,
面ABCD,
![]() 为棱
为棱![]() 的中点,M为线段
的中点,M为线段![]() 的中点.
的中点.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求三棱锥![]() 的体积.
的体积.

【答案】(1)见解析;(2) ![]() .
.
【解析】试题分析:(1)因为底面是菱形,所以AC⊥面BDD1B,又MF∥AC,所以MF⊥面BDD1B,即平面![]() 平面
平面![]() ;(2)过点B作BH⊥AD于H,可证出BH⊥平面ADD1A1,从而BH是三棱锥B﹣DD1F的高,求出△DD1F的面积,计算出三棱锥D1﹣BDF的体积.
;(2)过点B作BH⊥AD于H,可证出BH⊥平面ADD1A1,从而BH是三棱锥B﹣DD1F的高,求出△DD1F的面积,计算出三棱锥D1﹣BDF的体积.
试题解析:
(1)证明:∵底面是菱形,
∴AC⊥BD;
又∵B1B⊥面ABCD,AC面ABCD
∴AC⊥B1B,BD∩B1B=B,
∴AC⊥面BDD1B1
又∵MF∥AC,
∴MF⊥面BDD1B1;
又∵MF平面D1FB,
∴平面D1FB⊥平面BDD1B1;
(2)如图,过点B作BH⊥AD,垂足为H,
∵AA1⊥平面ABCD,BH平面ABCD,
∴BH⊥AA1,
∵AD、AA1是平面ADD1A1内的相交直线,
∴BH⊥平面ADD1A1,
在Rt△ABH中,∠DAB=60°,AB=AD=1,
∴BH=ABsin60°=![]() ,
,
∴三棱锥D1﹣BDF的体积为
V=![]() =
=![]() ×S△DD1FBH=
×S△DD1FBH=![]() ×
×![]() ×1×1×
×1×1×![]() =
=![]() .
.


 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:高中数学 来源: 题型:
【题目】某数学老师对本校2013届高三学生某次联考的数学成绩进行分析,按1:50进行分层抽样抽取20名学生的成绩进行分析,分数用茎叶图记录如图所示(部分数据丢失),得到的频率分布表如下: 
分数段(分) | [50,70] | [70,90] | [90,110] | [110,130] | [130,150] | 合计 |
频数 | b | |||||
频率 | a | 0.25 |
(1)表中a,b的值及分数在[90,100)范围内的学生,并估计这次考试全校学生数学成绩及格率(分数在[90,150]范围为及格);
(2)从大于等于110分的学生随机选2名学生得分,求2名学生的平均得分大于等于130分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四边形ABCD中, ![]() =(3,2),
=(3,2), ![]() =(x,y),
=(x,y), ![]() =(﹣2,﹣3)
=(﹣2,﹣3)
(1)若 ![]() ∥
∥ ![]() ,试求x与y满足的关系式;
,试求x与y满足的关系式;
(2)满足(1)同时又有 ![]() ⊥
⊥ ![]() ,求x,y的值及四边形ABCD的面积.
,求x,y的值及四边形ABCD的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形OQRP为矩形,其中P,Q分别是函数f(x)= ![]() sinwx(A>0,w>0)图象上的一个最高点和最低点,O为坐标原点,R为图象与x轴的交点.
sinwx(A>0,w>0)图象上的一个最高点和最低点,O为坐标原点,R为图象与x轴的交点. 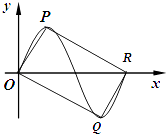
(1)求f(x)的解析式
(2)对于x∈[0,3],方程f2(x)﹣af(x)+1=0恒有四个不同的实数根,求实数a的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中日“钓鱼岛争端”问题越来越引起社会关注,我校对高一![]() 名学生进行了一次“钓鱼岛”知识测试,并从中抽取了部分学生的成绩,(满分
名学生进行了一次“钓鱼岛”知识测试,并从中抽取了部分学生的成绩,(满分![]() 分)作为样本,绘制了下面尚未完成的频率分布表和频率分布直方图.
分)作为样本,绘制了下面尚未完成的频率分布表和频率分布直方图.

(1)填写答题卡频率分布表中的空格, 补全频率分布直方图, 并标出每个小矩形对应的纵轴数据;
(2)请你估算该年级的平均数及中位数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com