
【题目】已知函数f(x)= ![]() ,x∈[-1,1],函数g(x)=[f(x)]2-2af(x)+3的最小值为h(a).
,x∈[-1,1],函数g(x)=[f(x)]2-2af(x)+3的最小值为h(a).
(1)求h(a).
(2)是否存在实数m>n>3,当h(a)的定义域为[n,m]时,值域为[n2,m2]?若存在,求出m,n的值;若不存在,说明理由.
【答案】(1) h(a)= 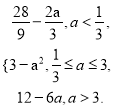 (2) 满足题意的m,n不存在.
(2) 满足题意的m,n不存在.
【解析】(1)∵x∈[-1,1],∴f(x)=![]() ∈
∈![]() .设t=
.设t=![]() ,t∈
,t∈![]() ,
,
则y=φ(t)=t2-2at+3=(t-a)2+3-a2.
当a<![]() 时,ymin=h(a)=φ
时,ymin=h(a)=φ![]() =
=![]() ;
;
当![]() ≤a≤3时,ymin=h(a)=φ(a)=3-a2;
≤a≤3时,ymin=h(a)=φ(a)=3-a2;
当a>3时,ymin=h(a)=φ(3)=12-6a.
∴h(a)=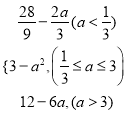
(2)假设满足题意的m、n存在,∵m>n>3,∴h(a)=12-6a在(3,+∞)上是减函数.∵h(a)的定义域为[n,m],值域为[n2,m2],∴![]() ,由②-①得6(m-n)=(m-n)(m+n),∵m>n>3,∴m+n=6,但这与“m>n>3”矛盾,∴满足题意的m、n不存在.
,由②-①得6(m-n)=(m-n)(m+n),∵m>n>3,∴m+n=6,但这与“m>n>3”矛盾,∴满足题意的m、n不存在.


科目:高中数学 来源: 题型:
【题目】为了预防流感,某学校对教室用药熏消毒法进行消毒.已知药物释放过程中,室内每立方米空气中的含药量![]() (毫克)与时间
(毫克)与时间![]() (小时)成正比;药物释放完毕后,
(小时)成正比;药物释放完毕后,![]() 与
与![]() 的函数关系式为
的函数关系式为![]() (
(![]() 为常数),如图所示.据图中提供的信息,回答下列问题:
为常数),如图所示.据图中提供的信息,回答下列问题:

(1)写出从药物释放开始,每立方米空气中的含药量![]() (毫克)与时间
(毫克)与时间![]() (小时)之间的函数关系式;
(小时)之间的函数关系式;
(2)据测定,当空气中每立方米的含药量降低到![]() 毫克以下时,学生方可进教室。那么药物释放开始,至少需要经过多少小时后,学生才能回到教室?
毫克以下时,学生方可进教室。那么药物释放开始,至少需要经过多少小时后,学生才能回到教室?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知幂函数![]() ,且
,且![]() 在
在![]() 上单调递增.
上单调递增.
(1)求实数![]() 的值,并写出相应的函数
的值,并写出相应的函数![]() 的解析式;
的解析式;
(2)若![]() 在区间
在区间![]() 上不单调,求实数
上不单调,求实数![]() 的取值范围;
的取值范围;
(3)试判断是否存在正数![]() ,使函数
,使函数![]() 在区间
在区间![]() 上的值域为
上的值域为![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙俩人各进行3次射击,甲每次击中目标的概率为 ![]() ,乙每次击中目标的概率为
,乙每次击中目标的概率为 ![]() . (Ⅰ)记甲恰好击中目标2次的概率;
. (Ⅰ)记甲恰好击中目标2次的概率;
(Ⅱ)求乙至少击中目标2次的概率;
(Ⅲ)求乙恰好比甲多击中目标2次的概率;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了5次试验,收集数据如下:
加工零件x(个) | 10 | 20 | 30 | 40 | 50 |
加工时间y(分钟) | 64 | 69 | 75 | 82 | 90 |
经检验,这组样本数据具有线性相关关系,那么对于加工零件的个数x与加工时间y这两个变量,下列判断正确的是( )
A.成正相关,其回归直线经过点(30,75)
B.成正相关,其回归直线经过点(30,76)
C.成负相关,其回归直线经过点(30,76)
D.成负相关,其回归直线经过点(30,75)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列几个命题正确的个数是( )
①若方程![]() 有一个正实根,一个负实根,则
有一个正实根,一个负实根,则![]() ;
;
②函数![]() 是偶函数,但不是奇函数;
是偶函数,但不是奇函数;
③设函数![]() 的定义域为
的定义域为![]() ,则函数
,则函数![]() 与函数
与函数![]() 图像关于
图像关于![]() 轴对称;
轴对称;
④一条曲线![]() 和直线
和直线![]() 的公共点个数是
的公共点个数是![]() ,则
,则![]() 的值不可能是1。
的值不可能是1。
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和Sn=1﹣nan(n∈N*)
(1)计算a1 , a2 , a3 , a4;
(2)猜想an的表达式,并用数学归纳法证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=2017x+sin2017x,g(x)=log2017x+2017x , 则( )
A.对于任意正实数x恒有f(x)≥g(x)
B.存在实数x0 , 当x>x0时,恒有f(x)>g(x)
C.对于任意正实数x恒有f(x)≤g(x)
D.存在实数x0 , 当x>x0时,恒有f(x)<g(x)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com