练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知=2，，，且，则·+·+·=         。


       

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    如图，曲线对应的函数是（      ）

       A．y=|sinx|   B．y=sin|x|   C．y=－sin|x|  D．y=－|sinx|

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某创业投资公司拟投资开发某种新能源产品，估计能获得10万元到1 000万元的投资收益．现准备制定一个对科研课题组的奖励方案：资金y(单位：万元)随投资收益x(单位：万元)的增加而增加，且奖金不超过9万元，同时奖金不超过投资收益的20%.

    (1)若建立函数y＝f(x)模型制定奖励方案，试用数学语言表述该公司对奖励函数f(x)模型的基本要求，并分析函数y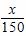＝＋2是否符合公司要求的奖励函数模型，并说明原因；

    (2)若该公司采用模型函数y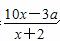＝作为奖励函数模型，试确定最小的正整数a的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知全集为R，集合M ={xlx2－2x－80），集合N={x|l－x<0}，则集合M（CRN）等于（  ）

        A．[-2,1]       B．（1,+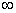）    C．[-l,4）      D．（1,4]

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知角的顶点与原点重合，始边与x轴的非负半轴重合，终边过点，则sin（2－）=（    ）

        A．    B．     C．   D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


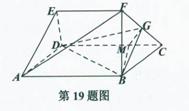
    如图几何体中，四边形ABCD为矩形，AB=3BC=6，EF =4，BF=CF=AE=DE=2，  EF∥AB，G为FC的中点，M为线段CD上的一点，且CM =2．

        （I）证明：平面BGM⊥平面BFC；

        （II）求三棱锥F－BMC的体积V．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某学生在高三学年最近九次考试中的数学成绩加下表：

      设回归直线方程y= bx+a，则点（a，b）在直线x+5y－10=0的（    ）

        A．左上方       B．左下方       C．右上方       D．右下方

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数．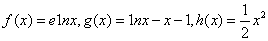

        （1）求函数g（x）的极大值；

        （2）求证：存在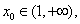，使；

        （3）对于函数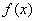与h（x）定义域内的任意实数x，若存在常数k、b使得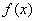≤kx +b和

             h（x）≥kx+b都成立，则称直线y=kx+b为函数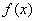与h（x）的分界线，试探究函数 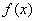与h（x）是否存在“分界线”？若存在，请给予汪明，并求出k、b的值：若不存在，请说明理由。

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知集合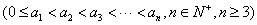，具有性质：对任意的，至少有一个属于.

    （Ⅰ）分别判断集合与是否具有性质；

    （Ⅱ）求证：①；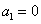

    ②；

    （Ⅲ）当或时集合中的数列是否一定成等差数列?说明理由.

    查看答案和解析>>

    同步练习册答案