
【题目】在平面直角坐标系xOy中,已知椭圆 ![]() +
+ ![]() =1(a>b>0)与双曲线
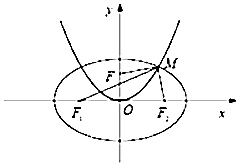
=1(a>b>0)与双曲线 ![]() ﹣y2=1有相同的焦点F1 , F2 , 抛物线x2=2py(p>0)的焦点为F,且与椭圆在第一象限的交点为M,若|MF1|+|MF2|=2
﹣y2=1有相同的焦点F1 , F2 , 抛物线x2=2py(p>0)的焦点为F,且与椭圆在第一象限的交点为M,若|MF1|+|MF2|=2 ![]() .
.
(1)求椭圆的方程;
(2)若|MF|= ![]() ,求抛物线的方程.
,求抛物线的方程.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】函数f(x)=x2+bx﹣1(b∈R).
(1)若函数y=f(x)在[1,+∞)上单调,求b的取值范围;
(2)若函数y=|f(x)|﹣2有四个零点,求b的取值范围;
(3)若函数y=|f(x)|在[0,|b|)上的最大值为g(b),求g(b)的表达式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx+ ![]() ,其中a为大于零的常数..
,其中a为大于零的常数..
(1)若函数f(x)在区间[1,+∞)内单调递增,求a的取值范围;
(2)求函数f(x)在区间[1,2]上的最小值;
(3)求证:对于任意的n∈N* , 且n>1时,都有lnn> ![]() +
+ ![]() +…+
+…+ ![]() 成立.
成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平行四边形ABCD的三个顶点的坐标为A(﹣1,5),B(﹣2,﹣1),C(2,3).
(1)求平行四边形ABCD的顶点D的坐标;
(2)在△ACD中,求CD边上的高所在直线方程;
(3)求四边形ABCD的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高一(1)班全体男生的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如图所示,据此解答如下问题:
(1)求该班全体男生的人数;
(2)求分数在![]() 之间的男生人数,并计算频率公布直方图中
之间的男生人数,并计算频率公布直方图中![]() 之间的矩形的高;
之间的矩形的高;

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点O为△ABC的外心,角A,B,C的对边分别满足a,b,c, (Ⅰ)若3 ![]() +4
+4 ![]() +5
+5 ![]() =
= ![]() ,求cos∠BOC的值;
,求cos∠BOC的值;
(Ⅱ)若 ![]()
![]() =
= ![]()
![]() ,求
,求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知圆
中,已知圆![]() 的方程是
的方程是![]() .
.
(![]() )如果圆
)如果圆![]() 与直线
与直线![]() 没有公共点,求实数
没有公共点,求实数![]() 的取值范围;
的取值范围;
(![]() )如果圆
)如果圆![]() 过坐标原点,过点
过坐标原点,过点![]() 直线
直线![]() 与圆
与圆![]() 交于
交于![]() ,
, ![]() 两点,记直线
两点,记直线![]() 的斜率的平方为
的斜率的平方为![]() ,对于每一个确定的
,对于每一个确定的![]() ,当
,当![]() 的面积最大时,用含
的面积最大时,用含![]() 的代数式表示
的代数式表示![]() ,并求
,并求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com