
【题目】已知点O为△ABC的外心,角A,B,C的对边分别满足a,b,c, (Ⅰ)若3 ![]() +4
+4 ![]() +5
+5 ![]() =
= ![]() ,求cos∠BOC的值;
,求cos∠BOC的值;
(Ⅱ)若 ![]()
![]() =
= ![]()
![]() ,求
,求 ![]() 的值.
的值.
【答案】解:(Ⅰ) 设外接圆半径为R,由3 ![]() +4
+4 ![]() +5
+5 ![]() =
= ![]() 得:4
得:4 ![]() +5
+5 ![]() =﹣3
=﹣3 ![]() ,平方得:16R2+40
,平方得:16R2+40 ![]()
![]() +25R2=9R2 , 即
+25R2=9R2 , 即 ![]()
![]() =﹣
=﹣ ![]() R2 ,
R2 ,
则cos∠BOC=﹣ ![]() ;
;
(Ⅱ)∵ ![]()
![]() =
= ![]()
![]() ,
,
∴ ![]() =
= ![]() ,
,
即: ![]() =
= ![]() ,
,
可得:﹣R2cos2A+R2cos2B=﹣R2cos2C+R2cos2A,
∴2cos2A=cos2C+cos2B,
即:2(1﹣2sin2A)=2﹣(2sin2B+2sin2C),
∴2sin2A=sin2B+sin2C,
∴利用正弦定理变形得:2a2=b2+c2 ,
∴ ![]() =2
=2
【解析】(Ⅰ)设三角形ABC的外接圆半径为R,将已知的等式变形后,左右两边平方,由O为三角形的外心,得到| ![]() |=|
|=| ![]() |=|
|=| ![]() |=R,再利用平面向量的数量积运算法则计算,可得出cos∠BOC的值;(Ⅱ)将已知的等式左右两边利用平面向量的减法法则计算,再利用平面向量的数量积运算法则变形,整理后利用二倍角的余弦函数公式化简,再利用正弦定理变形后,整理可得出所求式子的值.
|=R,再利用平面向量的数量积运算法则计算,可得出cos∠BOC的值;(Ⅱ)将已知的等式左右两边利用平面向量的减法法则计算,再利用平面向量的数量积运算法则变形,整理后利用二倍角的余弦函数公式化简,再利用正弦定理变形后,整理可得出所求式子的值.
【考点精析】认真审题,首先需要了解二倍角的余弦公式(二倍角的余弦公式:![]() ).
).


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源: 题型:
【题目】设命题p:x0∈(0,+∞),3 ![]() +x0=2016,命题q:a∈(0,+∞),f(x)=|x|﹣ax,(x∈R)为偶函数,那么,下列命题为真命题的是( )
+x0=2016,命题q:a∈(0,+∞),f(x)=|x|﹣ax,(x∈R)为偶函数,那么,下列命题为真命题的是( )
A.p∧q
B.(¬p)∧q
C.p∧(¬q)
D.(¬p)∧(¬q)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A(1,2),B(﹣3,﹣1),若圆x2+y2=r2(r>0)上恰有两点M,N,使得△MAB和△NAB的面积均为5,则r的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知椭圆 ![]() +
+ ![]() =1(a>b>0)与双曲线
=1(a>b>0)与双曲线 ![]() ﹣y2=1有相同的焦点F1 , F2 , 抛物线x2=2py(p>0)的焦点为F,且与椭圆在第一象限的交点为M,若|MF1|+|MF2|=2
﹣y2=1有相同的焦点F1 , F2 , 抛物线x2=2py(p>0)的焦点为F,且与椭圆在第一象限的交点为M,若|MF1|+|MF2|=2 ![]() .
.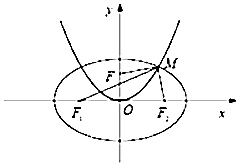
(1)求椭圆的方程;
(2)若|MF|= ![]() ,求抛物线的方程.
,求抛物线的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设点P为有公共焦点F1 , F2的椭圆和双曲线的一个交点,且cos∠F1PF2= ![]() ,椭圆的离心率为e1 , 双曲线的离心率为e2 , 若e2=2e1 , 则e1=( )
,椭圆的离心率为e1 , 双曲线的离心率为e2 , 若e2=2e1 , 则e1=( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》中有“今有五人分无钱,令上二人所得与下三人等,问各得几何?”.其意思为“已知甲、乙、丙、丁、戊五人分5钱,甲、乙两人所得与丙、丁、戊三人所得相同,且甲、乙、丙、丁、戊所得依次成等差数列,问五人各得多少钱?”这个问题中,甲所得为( )
A.![]() 钱
钱
B.![]() 钱
钱
C.![]() 钱
钱
D.![]() 钱
钱
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在等差数列{an}中,2a9=a12+13,a2=5,其前n项和为Sn .
(1)求数列{an}的通项公式;
(2)求数列{ ![]() }的前n项和Tn , 并证明Tn<
}的前n项和Tn , 并证明Tn< ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,某镇有一块空地![]() ,其中
,其中![]() ,
, ![]() ,
, ![]() 。当地镇政府规划将这块空地改造成一个旅游景点,拟在中间挖一个人工湖
。当地镇政府规划将这块空地改造成一个旅游景点,拟在中间挖一个人工湖![]() ,其中
,其中![]() 都在边
都在边![]() 上,且
上,且![]() ,挖出的泥土堆放在
,挖出的泥土堆放在![]() 地带上形成假山,剩下的
地带上形成假山,剩下的![]() 地带开设儿童游乐场. 为安全起见,需在
地带开设儿童游乐场. 为安全起见,需在![]() 的周围安装防护网.
的周围安装防护网.
(1)当![]() 时,求防护网的总长度;
时,求防护网的总长度;
(2)若要求挖人工湖用地![]() 的面积是堆假山用地
的面积是堆假山用地![]() 的面积的
的面积的![]() 倍,试确定
倍,试确定![]() 的大小;
的大小;
(3)为节省投入资金,人工湖![]() 的面积要尽可能小,问如何设计施工方案,可使
的面积要尽可能小,问如何设计施工方案,可使![]() 的面积最小?最小面积是多少?
的面积最小?最小面积是多少?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com