
【题目】第一届“一带一路”国际合作高峰论坛于2017年5月14日至15日在北京举行,这是2017年我国重要的主场外交活动,对推动国际和地区合作具有重要意义.某高中政教处为了调查学生对“一带一路”的关注情况,在全校组织了“一带一路知多少”的知识问卷测试,并从中随机抽取了12份问卷,得到其测试成绩(百分制),如茎叶图所示.
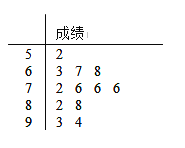
(1)写出该样本的众数、中位数,若该校共有3000名学生,试估计该校测试成绩在70分以上的人数;
(2)从所抽取的70分以上的学生中再随机选取4人.
①记![]() 表示选取4人的成绩的平均数,求
表示选取4人的成绩的平均数,求![]() ;
;
②记![]() 表示测试成绩在80分以上的人数,求
表示测试成绩在80分以上的人数,求![]() 的分布和数学期望.
的分布和数学期望.
【答案】(1)![]() ;(2)①
;(2)①![]() ,②
,②![]() .
.
【解析】试题分析:(1)众数为![]() ,中位数为
,中位数为![]() ,抽取的
,抽取的![]() 人中,
人中, ![]() 分以下的有
分以下的有![]() 人,不低于
人,不低于![]() 分的有
分的有![]() 人,从而求出从该校学生中任选
人,从而求出从该校学生中任选![]() 人,这个人测试成绩在
人,这个人测试成绩在![]() 分以上的概率,由此能求出该校这次测试成绩在
分以上的概率,由此能求出该校这次测试成绩在![]() 分以上的人数;(2)①由题意知
分以上的人数;(2)①由题意知![]() 分以上的有
分以上的有![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,当所选取的四个人的成绩的平均分大于
,当所选取的四个人的成绩的平均分大于![]() 分时,有两类:一类是:
分时,有两类:一类是: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,共1种;另一类是:
,共1种;另一类是: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,共3种.由此能求出
,共3种.由此能求出![]() ;②由题意得
;②由题意得![]() 的可能取值为0,1,2,3,4,分别求出相应的概率,由此能求出
的可能取值为0,1,2,3,4,分别求出相应的概率,由此能求出![]() 的分布列和
的分布列和![]() .
.
试题解析:(1)众数为76,中位数为76.抽取的12人中,70分以下的有4人,不低于70分的有8人,故从该校学生中人选1人,这个人测试成绩在70分以上的概率为![]() ,故该校这次测试成绩在70分以上的约有
,故该校这次测试成绩在70分以上的约有![]() (人)
(人)
(2)①由题意知70分以上的有72,76,76,76,82,88,93,94.
当所选取的四个人的成绩的平均分大于87分时,有两类.
一类是82,88,93,94,共1种;
另一类是76,88,93,94,共3种.所以 ![]() .
.
②由题意可得, ![]() 的可能取值为0,1,2,3,4
的可能取值为0,1,2,3,4
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]() 的分别列为
的分别列为
| 0 | 1 | 2 | 3 | 4 |
|
|
|
|
|
|
![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】下列推理过程不是演绎推理的是( ).
①一切奇数都不能被2整除,2019是奇数, 2019不能被2整除;
②由“正方形面积为边长的平方”得到结论:正方体的体积为棱长的立方;
③在数列![]() 中,
中,![]() ,
,![]() ,由此归纳出
,由此归纳出![]() 的通项公式;
的通项公式;
④由“三角形内角和为![]() ”得到结论:直角三角形内角和为
”得到结论:直角三角形内角和为![]() .
.
A. ① ② B. ② ③ C. ③ ④ D. ②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以直角坐标系的原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴,并在两种坐标系中取相同的长度单位,已知直线
轴正半轴为极轴,并在两种坐标系中取相同的长度单位,已知直线![]() 的参数方程为
的参数方程为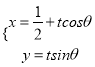 ,(
,( ![]() 为参数,
为参数, ![]() ),曲线
),曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
, ![]() 两点,当
两点,当![]() 变化时,求
变化时,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假设每一架飞机的引擎在飞行中出现故障率为![]() ,且各引擎是否有故障是独立的,已知4引擎飞机中至少有3个引擎正常运行,飞机就可成功飞行;2引擎飞机要2个引擎全部正常运行,飞机也可成功飞行,要使4引擎飞机比2引擎飞机更安全,则
,且各引擎是否有故障是独立的,已知4引擎飞机中至少有3个引擎正常运行,飞机就可成功飞行;2引擎飞机要2个引擎全部正常运行,飞机也可成功飞行,要使4引擎飞机比2引擎飞机更安全,则![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3+3|x﹣a|(a∈R).
(1)若f(x)在[﹣1,1]上的最大值和最小值分别记为M(a),m(a),求M(a)﹣m(a);
(2)设b∈R,若[f(x)+b]2≤4对x∈[﹣1,1]恒成立,求3a+b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知菱形ABCD的边长为2,∠BAD=120°,点E、F分别在边BC、DC上, ![]() =λ
=λ ![]() ,
, ![]() =μ
=μ ![]() ,若
,若 ![]()
![]() =1,
=1, ![]()
![]() =﹣
=﹣ ![]() ,则λ+μ=( )
,则λ+μ=( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
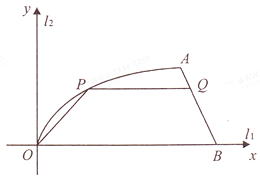
【题目】如图,某小区内有两条互相垂直的道路![]() 与
与![]() ,平面直角坐标系
,平面直角坐标系![]() 的第一象限有一块空地
的第一象限有一块空地![]() ,其边界
,其边界![]() 是函数
是函数![]() 的图象,前一段曲线
的图象,前一段曲线![]() 是函数
是函数![]() 图象的一部分,后一段
图象的一部分,后一段![]() 是一条线段.测得
是一条线段.测得![]() 到
到![]() 的距离为8米,到
的距离为8米,到![]() 的距离为16米,
的距离为16米,![]() 长为20米.
长为20米.
(1)求函数![]() 的解析式;
的解析式;
(2)现要在此地建一个社区活动中心,平面图为梯形![]() (其中
(其中![]() ,
,![]() 为两底边),问:梯形的高为多少米时,该社区活动中心的占地面积最大,并求出最大面积.
为两底边),问:梯形的高为多少米时,该社区活动中心的占地面积最大,并求出最大面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对于直线l:ax+by+c=0和点P1(x1 , y1),P2(x2 , y2),记η=(ax1+by1+c)(ax2+by2+c),若η<0,则称点P1 , P2被直线l分隔,若曲线C与直线l没有公共点,且曲线C上存在点P1、P2被直线l分隔,则称直线l为曲线C的一条分隔线.
(1)求证:点A(1,2),B(﹣1,0)被直线x+y﹣1=0分隔;
(2)若直线y=kx是曲线x2﹣4y2=1的分隔线,求实数k的取值范围;
(3)动点M到点Q(0,2)的距离与到y轴的距离之积为1,设点M的轨迹为曲线E,求证:通过原点的直线中,有且仅有一条直线是E的分隔线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com