
| A. | 8 | B. | 8+4$\sqrt{3}$ | C. | 6 | D. | 6+4$\sqrt{3}$ |
分析 由三角形面积公式求得bc的值,利用余弦定理求得a的值,三角形周长的表达式,根据基本不等式求得a+b+c的最小值.
解答 解:S△ABC=$\frac{1}{2}$bcsinA,即$4\sqrt{3}$=$\frac{1}{2}$bcsin120°,解得bc=16,
由余弦定理可知:a2=b2+c2-2bccosA,
得a2=(b+c)2-16,
∴L△ABC=a+b+c=$\sqrt{(b+c)^{2}-16}$+b+c≥$\sqrt{4bc-16}$+$2\sqrt{bc}$=8+4$\sqrt{3}$,
当且仅当b=c=4时取等号.
故答案选:B.
点评 本题考查三角形面积公式,余弦定理及利用基本不等式求最值,属于基础题.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
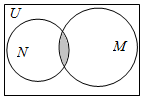 设全集U=C(复数集),i是虚数单位,集合M=Z(整数集)和N={i,i2,$\frac{1-i}{1+i}$,$\frac{(1+i)^{2}}{i}$}的关系韦恩(Venn)如图所示,则阴影部分所表示的集合是( )
设全集U=C(复数集),i是虚数单位,集合M=Z(整数集)和N={i,i2,$\frac{1-i}{1+i}$,$\frac{(1+i)^{2}}{i}$}的关系韦恩(Venn)如图所示,则阴影部分所表示的集合是( )| A. | ∅ | B. | {-1} | C. | {-1,2} | D. | {-1,1,2} |
查看答案和解析>>
科目:高中数学 来源:2016-2017学年广东清远三中高二上学期月考一数学(文)试卷(解析版) 题型:解答题
已知首项为 的等比数列
的等比数列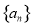 不是递减数列, 其前
不是递减数列, 其前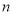 项和为
项和为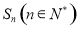 ,且
,且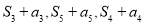 成等差数列.
成等差数列.
(1)求数列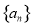 通项公式;
通项公式;
(2)设 ,求数列
,求数列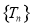 的最大项的值与最小项的值.
的最大项的值与最小项的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com