
【题目】定义在R上的函数![]() 满足
满足![]() ,且对任意的
,且对任意的![]() 都有
都有![]() 其中
其中![]() 为
为![]() 的导数
的导数![]() ,则下列一定判断正确的是( )
,则下列一定判断正确的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
【答案】B
【解析】
根据条件对任意的x≥1都有,f′(x)+2f(x)>0,构造函数F(x)=e2xf(x),则F'(x)=2e2xf(x)+e2xf'(x)=e2x[2f(x)+f'(x)],可得F(x)在x≥1时单调递增.由e4(x+1)f(x+2)=f(﹣x),注意到F(x+2)=e2(x+2)f(x+2); F(﹣x)=e﹣2xf(﹣x);代入已知表达式可得:F(x+2)=F(﹣x),所以F(x)关于x=1对称,则由F(x)在x≥1时单调递增,化简即可得出结果.
设F(x)=e2xf(x),则F'(x)=2e2xf(x)+e2xf'(x)=e2x[2f(x)+f'(x)],
∵对任意的x≥1都有f′(x)+2f(x)>0;
则F'(x)>0,则F(x)在[1,+∞)上单调递增;
F(x+2)=e2(x+2)f(x+2); F(﹣x)=e﹣2xf(﹣x);
因为e4(x+1)f(x+2)=f(﹣x),
∴e2xe2x+2f(x+2)=f(﹣x);∴e2x+2f(x+2)=e﹣2xf(﹣x)
∴F(x+2)=F(﹣x),所以F(x)关于x=1对称,则F(﹣2)=F(4),
∵F(x)在[1,+∞)上单调递增;
∴F(3)<F(4)即F(3)<F(﹣2),∴e6f(3)<e﹣4f(﹣2);
即e10f(3)<f(﹣2)成立.故D不正确;
F(3)=F(﹣1),F(0)=F(2)故A,C 均错误;
F(3)>F(2)∴e2f(3)>f(2).B正确.
故选:B.


 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案科目:高中数学 来源: 题型:
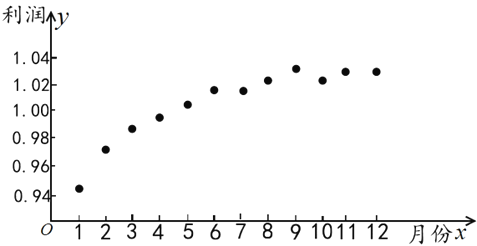
【题目】如图是某创业公司2017年每月份公司利润(单位:百万元)情况的散点图:为了预测该公司2018年的利润情况,根据上图数据,建立了利润y与月份x的两个线性回归模型:①![]() 0.94+0.028
0.94+0.028![]() ;②
;②![]() 0.96+0.032lnx,并得到以下统计值:
0.96+0.032lnx,并得到以下统计值:
模型① | 模型② | |
残差平方和 | 0.000591 | 0.000164 |
总偏差平方和 | 0.006050 | |
(1)请利用相关指数R2判断哪个模型的拟合效果更好;
(2)为了激励员工工作的积极性,公司每月会根据利润的情况进行奖惩,假设本月利润为y1,而上一月利润为y2,计算z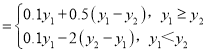 ,并规定:若z≥10,则向全体员工发放奖金总额z元;若z<10,从全体员工每人的工资中倒扣10﹣z元作为惩罚,扣完为止,请根据(1)中拟合效果更好的回归模型,试预测208年4月份该公司的奖惩情况?(结果精确到小数点后两位)
,并规定:若z≥10,则向全体员工发放奖金总额z元;若z<10,从全体员工每人的工资中倒扣10﹣z元作为惩罚,扣完为止,请根据(1)中拟合效果更好的回归模型,试预测208年4月份该公司的奖惩情况?(结果精确到小数点后两位)
参考数据及公式:![]() 1.73,
1.73,![]() 2.24,1n2≈0.69,1n3≈1.10,ln5≈1.61.相关指数R2=1
2.24,1n2≈0.69,1n3≈1.10,ln5≈1.61.相关指数R2=1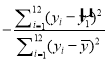 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() ,过点
,过点![]() 作直线
作直线![]() 和曲线
和曲线![]() 交于
交于![]() 、
、![]() 两点.
两点.
(1)求曲线![]() 的焦点到它的渐近线之间的距离;
的焦点到它的渐近线之间的距离;
(2)若![]() ,点
,点![]() 在第一象限,
在第一象限,![]() 轴,垂足为
轴,垂足为![]() ,连结
,连结![]() ,求直线
,求直线![]() 倾斜角的取值范围;
倾斜角的取值范围;
(3)过点![]() 作另一条直线
作另一条直线![]() ,
,![]() 和曲线
和曲线![]() 交于
交于![]() 、
、![]() 两点,问是否存在实数
两点,问是否存在实数![]() ,使得
,使得![]() 和
和![]() 同时成立?如果存在,求出满足条件的实数
同时成立?如果存在,求出满足条件的实数![]() 的取值集合,如果不存在,请说明理由.
的取值集合,如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为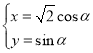 (
(![]() 为参数).在以
为参数).在以![]() 为极点,
为极点,![]() 轴正半轴为极轴的极坐标系中,直线
轴正半轴为极轴的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求曲线![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设点![]() ,若直线
,若直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() 为常数.
为常数.
(1)当![]() 时,解不等式
时,解不等式![]() ;
;
(2)已知![]() 是以2为周期的偶函数,且当
是以2为周期的偶函数,且当![]() 时,有
时,有![]() .若
.若![]() ,且
,且![]() ,求函数
,求函数![]()
![]() 的反函数;
的反函数;
(3)若在![]() 上存在
上存在![]() 个不同的点
个不同的点![]() ,
,![]() ,使得
,使得![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
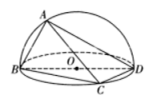
【题目】如图,已知![]() 是圆
是圆![]() 的直径,
的直径,![]() ,
,![]() 在圆上且分别在
在圆上且分别在![]() 的两侧,其中
的两侧,其中![]() ,
,![]() .现将其沿
.现将其沿![]() 折起使得二面角
折起使得二面角![]() 为直二面角,则下列说法不正确的是( )
为直二面角,则下列说法不正确的是( )
A.![]() ,
,![]() ,
,![]() ,
,![]() 在同一个球面上
在同一个球面上
B.当![]() 时,三棱锥
时,三棱锥![]() 的体积为
的体积为![]()
C.![]() 与
与![]() 是异面直线且不垂直
是异面直线且不垂直
D.存在一个位置,使得平面![]() 平面
平面![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com