【题目】如图，在多面体
中，侧棱
、
、
、
都和平面
垂直，
，
，
，
.
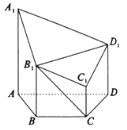
（1）证明：平面
平面
；
（2）求多面体的体积.
【答案】（1）见解析；（2）
.
【解析】
（1）连接
，证明出四边形
是平行四边形，可得出
，证明出
平面
，可得出
平面，再利用平面与平面垂直的判定定理可得出平面
平面；
（2）平面
把多面体分成两部分，多面体
可分为一个三棱锥和一个三棱柱，多面体
可看成三棱柱
截去三棱锥
，计算出两个多面体的体积，相加即可.
（1）连接，由题设
，
，所以四边形是平行四边形，所以.
由题设，四边形
是等腰梯形，取
中点
，连接
、
，
因为
，
，所以四边形
是平行四边形，
，所以
，得到
，因此
.
又由题设，
平面
，且
平面，
，
又
，所以平面，又（已证），
所以平面，而
平面
，因此平面平面；
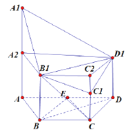
（2）如图，平面把多面体分成两部分，分别计算.
易求
，
，多面体可分为一个三棱锥和一个三棱柱，多面体可看成三棱柱截去三棱锥.
.
阅读快车系列答案科目：高中数学 来源： 题型：
【题目】如题所示:扇形ABC是一块半径为2千米，圆心角为60°的风景区，P点在弧BC上，现欲在风景区中规划三条三条商业街道PQ、QR、RP，要求街道PQ与AB垂直，街道PR与AC垂直，直线PQ表示第三条街道。
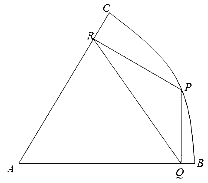
(1)如果P位于弧BC的中点，求三条街道的总长度；
(2)由于环境的原因，三条街道PQ、PR、QR每年能产生的经济效益分别为每千米300万元、200万元及400万元，问:这三条街道每年能产生的经济总效益最高为多少？(精确到1万元)
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】至
年底，我国发明专利申请量已经连续
年位居世界首位，下表是我国
年至年发明专利申请量以及相关数据.
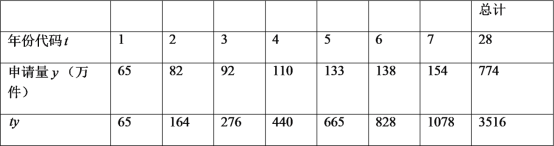
注：年份代码
～
分别表示～.
（1）可以看出申请量每年都在增加，请问这几年中哪一年的增长率达到最高，最高是多少？
（2）建立
关于
的回归直线方程（精确到
），并预测我国发明专利申请量突破
万件的年份.
参考公式：回归直线的斜率和截距的最小二乘法估计分别为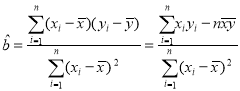
，
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】关于函数
＝|cosx|+cos|2x|有下列四个结论：①是偶函数；②π是的最小正周期；③在[
π，
π]上单调递增；④的值域为[﹣2，2]．上述结论中，正确的个数为（ ）
A.1B.2C.3D.4
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知极点与坐标原点
重合，极轴与
轴非负半轴重合，
是曲线
上任一点
满足
，设点的轨迹为
.
（1）求曲线的平面直角坐标方程；
（2）将曲线向右平移
个单位后得到曲线
，设曲线与直线
（
为参数）相交于
、
两点，记点
，求
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
