
分析 (Ⅰ)从装有2个红球A1,A2和2个白球B1,B2的甲箱与装有3个红球a1,a2,a3和1个白球b1的乙箱中,各随机摸出1个球,利用列举法能求出所有可能的摸出结果.
(Ⅱ)所有可能的摸出结果共16种,利用列举法求出摸出的2个球都是红球的结果有6种,分别求出中奖的概率和不中奖的概率,由此能求出中奖的概率大于不中奖的概率这种说法不正确.
解答 解:(Ⅰ)从装有2个红球A1,A2和2个白球B1,B2的甲箱与装有3个红球a1,a2,a3和1个白球b1的乙箱中,
各随机摸出1个球,所有可能的摸出结果是:
{A1,a1},{A1,a2},{A1,a3},{A1,b1},{A2,a1},{A2,a2},{A2,a3},{A2,b1},
{B1,a1},{B1,a2},{B1,a3},{B1,b1},{B2,a1},{B2,a2},{B2,a3},{B2,b1}. …(6分)
(Ⅱ)有人认为:两个箱子中的红球比白球多,所以中奖的概率大于不中奖的概率,这不正确,理由如下:…(7分)
由(I)知,所有可能的摸出结果共16种,…(8分)
其中摸出的2个球都是红球的结果为:
{A1,a1},{A1,a2},{A1,a3},{A2,a1},{A2,a2},{A2,a3},共6种,…(9分)
故中奖的概率为$P=\frac{6}{16}=\frac{3}{8}$,
不中奖的概率为$1-\frac{3}{8}=\frac{5}{8}$$>\frac{3}{8}$,…(11分)
故中奖的概率大于不中奖的概率这种说法不正确.…(12分)
点评 本题考查概率的求法及应用,是基础题,解题时要认真审题,注意列举法的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
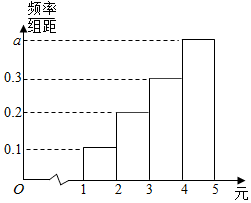 甲、乙、丙三人参加微信群抢红包游戏,规则如下:每轮游戏发10个红包,每个红包金额在[1,5]产生.已知在每轮游戏中所产生的10个红包金额的频率分布直方图如图所示.
甲、乙、丙三人参加微信群抢红包游戏,规则如下:每轮游戏发10个红包,每个红包金额在[1,5]产生.已知在每轮游戏中所产生的10个红包金额的频率分布直方图如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com