
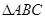 的外接圆半径
的外接圆半径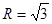 ,角
,角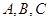 的对边分别是
的对边分别是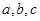 ,且
,且
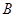 和边长
和边长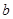 ;
;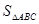 的最大值及取得最大值时的
的最大值及取得最大值时的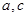 的值,并判断此时三角形的形状.
的值,并判断此时三角形的形状.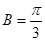 ,
,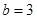 ;(2)
;(2)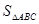 的最大值
的最大值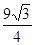 ,此时
,此时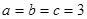 ,此时三角形是等边三角形.
,此时三角形是等边三角形.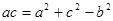 ,再利用余弦定理求
,再利用余弦定理求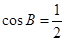 ,在
,在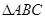 中,
中,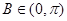 ,所以
,所以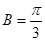 ,再利用正弦定理求边
,再利用正弦定理求边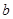 ;第二问,先通过余弦定理
;第二问,先通过余弦定理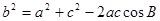 ,再结合基本不等式求出
,再结合基本不等式求出 的最大值,得到面积的最大值,注意等号成立的条件,通过这个条件得出
的最大值,得到面积的最大值,注意等号成立的条件,通过这个条件得出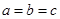 ,所以判断三角形形状为等边三角形.
,所以判断三角形形状为等边三角形.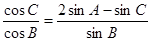 ,得:
,得: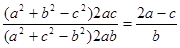 ,
,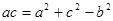 ,所以
,所以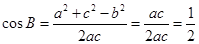 , 4分
, 4分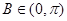 ,所以
,所以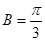 ,又
,又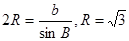 ,所以
,所以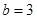 6分
6分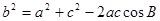 ,
,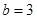 ,
,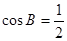
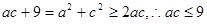
 (当且仅当
(当且仅当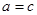 时取等号) 8分
时取等号) 8分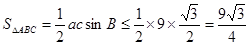 (当且仅当
(当且仅当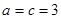 时取等号) 10分
时取等号) 10分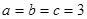
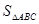 的最大值
的最大值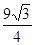 ,取得最大值时,此时三角形是等边三角形. 12分
,取得最大值时,此时三角形是等边三角形. 12分

 天天向上口算本系列答案
天天向上口算本系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com