练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    5．若方程x2-x+m=0有两个不等正根，则实数m的取值范围是（0，$\frac{1}{4}$）．

    分析 若方程x2-x+m=0有两个不等正根，则$\left\{\begin{array}{l}△=1-4m＞0\\{x}_{1}{x}_{2}=m＞0\end{array}\right.$，解得实数m的取值范围．

    解答 解：若方程x2-x+m=0有两个不等正根，
    则$\left\{\begin{array}{l}△=1-4m＞0\\{x}_{1}{x}_{2}=m＞0\end{array}\right.$，
    解得：m∈（0，$\frac{1}{4}$），
    故答案为：（0，$\frac{1}{4}$）

    点评 本题考查的知识点是二次函数的图象图象和性质，熟练掌握二次函数的图象和性质，是解答的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    1．函数f（x）=$lo{g}_{{2}_{\;}}$（-x2+2x+3）的单调递增区间是（-1，1）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．已知函数f（x）=1-$\frac{2}{1{0}^{x}+1}$．
    （1）判断函数f（x）的奇偶性；
    （2）求f（x）的值域；
    （3）用定义证明f（x）在（-∞，+∞）上的单调性．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．终边在第二象限的角的集合可以表示为（　　）
    A．{α|90°＜α＜180°}
    B．{α|90°+k•180°＜α＜180°+k•180°，k∈Z}
    C．{α|-270°+k•180°＜α＜-180°+k•180°，k∈Z}
    D．{α|-270°+k•360°＜α＜-180°+k•360°，k∈Z}

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．已知集合A={x|x＜-1或x＞2}，B={1，4a，a2}，C={x|a＜x＜a+4}．
    （1）若4∈B，求A∩B；
    （2）若∁RC⊆A，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．已知两条直线m，n和平面α，那么下列命题中的真命题为（　　）
    A．若m∥n，n?α，则m∥αB．若m⊥n，n?α，则m⊥α
    C．若m∥n，n?α，m?α，则m∥αD．若m⊥n，n?α，m?α，则m⊥α

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．代数式sin120°cos240°的值为（　　）
    A．$-\frac{3}{4}$B．$-\frac{{\sqrt{3}}}{4}$C．$-\frac{3}{2}$D．$-\frac{1}{4}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

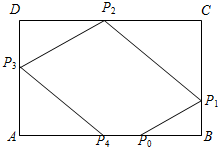    14．如图，矩形ABCD中，AB=3，AD=2，一质点从AB边上的点P0出发，沿与AB的夹角为θ的方向射到边BC上点P1后，依次反射（入射角与反射角相等）到边CD，DA和AB上的P2，P3，P4处．
    （1）若P4与P0重合，求tanθ的值；
    （2）若P4落在A、P0两点之间，且AP0=2，设tanθ=t．
    （i）求tanθ的取值范围；
    （ii）将五边形P0P1P2P3P4的面积S表示为t的函数，并求S的最大值．
    （参考结论：函数g（x）=x+$\frac{a}{x}$，（a＞0），x＞0，则函数g（x）在（0，$\sqrt{a}$]上是减函数，在[$\sqrt{a}$，+∞）是增函数．）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    15．已知函数f（x）=-x2+2bx+c，任意的x1，x2∈（-∞，0）且x1≠x2时，都有$\frac{{f（{x_1}）-f（{x_2}）}}{{{x_2}-{x_1}}}$＜0，则实数b的取值范围为b≥0．

    查看答案和解析>>

    同步练习册答案