解(1)因为当x∈(0,π]时,g'(x)=cosx-xsinx-cosx=-xsinx≤0,
所以g(x)在(0,π]上单调递减,(3分)
又g(0)=0,所以当x∈(0,π]时,g(x)<0(4分)
(2)因为
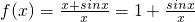
,
所以

,
由(1)知,当x∈(0,π]时,xcosx-sinx<0,所以f'(x)<0(6分)
所以f(x)在(0,π]上单调递减,则当x∈(0,π]时,f(x)
min=f(π)=1(8分)
由题意知,f(x)<a在(0,π]上有解,所以a>f(x)
min,从而a>1(10分)
(3)由g(bx)≤bxcosbx-bsinx(b≥-1),得sinbx≥bsinx(b≥-1)对x∈(0,π]恒成立,
①当b=-1,0,1时,不等式显然成立(11分)
②当b>1时,因为bx∈(0,bπ],所以取
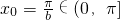
,
则有sinbx
0=0<bsinx
0,从而时不等式不恒成立(12分)
③当0<b<1时,由(Ⅱ)可知
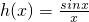
在(0,π]上单调递减,而0<bx<x≤π,
∴

,
∴sinbx>bsinx成立(14分)
④当-1<b<0时,当x∈(0,π]时,0<-bx<x≤π,
则
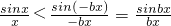
,∴sinbx<bsinx不成立,
综上所述,当b=-1或0≤b≤1时,有g(bx)≤bxcosbx-bsinx(b≥-1)对x∈(0,π]恒成立.(16分)
分析:(1)转化求函数g(x)在(0,π]上的最大值,利用函数的导数判断单调性进而求解;
(2)依题意即转化为求函数f(x)在(0,π]上的最小值,利用函数的导数判断单调性进而求解;
(3)先表示出函数g(bx),将恒成立问题转化为函数求最值问题,利用函数的导数判断单调性进而求解,注意b的范围的讨论.
点评:本题考查用导数研究函数的单调区间以及根据函数的增减性求得到函数的最值,掌握不等式恒成立时所取的条件,“转化”是这类题目解决的“灵魂”.

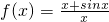 ,g(x)=xcosx-sinx.
,g(x)=xcosx-sinx.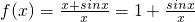 ,
, ,
,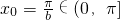 ,
,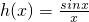 在(0,π]上单调递减,而0<bx<x≤π,
在(0,π]上单调递减,而0<bx<x≤π, ,
,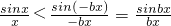 ,∴sinbx<bsinx不成立,
,∴sinbx<bsinx不成立,

 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案