
【题目】下列各组函数是同一函数的是
①![]() 与
与![]() ; ②
; ②![]() 与
与![]() ;
;
③![]() 与
与![]() ; ④
; ④![]() 与
与![]()
A. ②③ B. ①③ C. ③④ D. ①④
【答案】C
【解析】
①![]() 与
与![]() 定义域相同,但是对应法则不同;②f(x)=x与g(x)对应法则不同,不是同一函数;③f(x)=x0与
定义域相同,但是对应法则不同;②f(x)=x与g(x)对应法则不同,不是同一函数;③f(x)=x0与![]() 定义域相同,对应法则相同,是同一函数;④f(x)=x2﹣x﹣1与g(t)=t2﹣t﹣1.函数与用什么字母表示无关,只与定义域和对应法则有关.
定义域相同,对应法则相同,是同一函数;④f(x)=x2﹣x﹣1与g(t)=t2﹣t﹣1.函数与用什么字母表示无关,只与定义域和对应法则有关.
解:①![]() 与
与![]() 的定义域是{x:x≤0};而
的定义域是{x:x≤0};而![]() x
x![]() ,对应法则不相同,故这两个函数不是同一函数;
,对应法则不相同,故这两个函数不是同一函数;
②f(x)=x与![]() 的定义域都是R,
的定义域都是R,![]() |x|,这两个函数的定义域相同,对应法则不相同,故这两个函数不是同一函数;
|x|,这两个函数的定义域相同,对应法则不相同,故这两个函数不是同一函数;
③f(x)=x0=1的定义域是{x:x≠0},而![]() =1的定义域是{x:x≠0},故这两个函数是同一函数;
=1的定义域是{x:x≠0},故这两个函数是同一函数;
④f(x)=x2﹣x﹣1与g(t)=t2﹣t﹣1,定义域与对应法则相同,是同一函数.
故选:C.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:高中数学 来源: 题型:
【题目】如图,某机器人的运动轨道是边长为1米的正三角形ABC,开机后它从A点出发,沿轨道先逆时针运动再顺时针运动,每运动6米改变一次运动方向(假设按此方式无限运动下去),运动过程中随时记录逆时针运动的总路程s1和顺时针运动的总路程s2,x为该机器人的“运动状态参数”,规定:逆时针运动时x=s1,顺时针运动时x=-s2,机器人到A点的距离d与x满足函数关系d=f(x),现有如下结论:
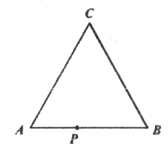
①f(x)的值域为[0,1];
②f(x)是以3为周期的函数;
③f(x)是定义在R上的奇函数;
④f(x)在区间[-3,-2]上单调递增.
其中正确的有_________(写出所有正确结论的编号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示几何体ABC﹣A1B1C1中,A1、B1、C1在面ABC上的射影分别是线段AB、BC、AC的中点,面A1B1C1∥面ABC,△ABC是边长为2的等边三角形. 
(1)求证:△A1B1C1是等边三角形;
(2)若面ACB1A1⊥面BA1B1 , 求该几何体ABC﹣A1B1C1的体积;
(3)在(2)的条件下,求面ABC与面A1B1B所成的锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1=1,an+1=3an+1.
(1)证明{an+ ![]() }是等比数列,并求{an}的通项公式;
}是等比数列,并求{an}的通项公式;
(2)证明: ![]() +
+ ![]() +…+
+…+ ![]() <
< ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 的离心率为
的离心率为![]() ,点
,点![]() 在椭圆C上.
在椭圆C上.
(1)求椭圆C的方程;
(2)设动直线![]() 与椭圆C有且仅有一个公共点,判断是否存在以原点O为圆心的圆,满足此圆与
与椭圆C有且仅有一个公共点,判断是否存在以原点O为圆心的圆,满足此圆与![]() 相交两点
相交两点![]() ,
,![]() (两点均不在坐标轴上),且使得直线
(两点均不在坐标轴上),且使得直线![]() ,
,![]() 的斜率之积为定值?若存在,求此圆的方程;若不存在,说明理由.
的斜率之积为定值?若存在,求此圆的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() (a∈R).
(a∈R).
(Ⅰ)若f(1)=2,求函数y=f(x)-2x在[![]() ,2]上的值域;
,2]上的值域;
(Ⅱ)当a∈(0,![]() )时,试判断f(x)在(0,1]上的单调性,并用定义证明你的结论.
)时,试判断f(x)在(0,1]上的单调性,并用定义证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com