
(14分)设函数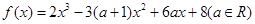
 处取得极值
处取得极值
(1)求常数a的值;
(2)求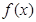 在R上的单调区间;
在R上的单调区间;
(3)求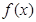 在
在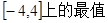 。
。
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:高中数学 来源:2010-2011学年山东省济宁市任城一中高二下学期期末考试文科数学 题型:解答题
(14分)设函数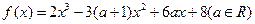
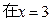 处取得极值
处取得极值
(1)求常数a的值;
(2)求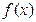 在R上的单调区间;
在R上的单调区间;
(3)求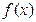 在
在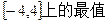 。
。
查看答案和解析>>
科目:高中数学 来源:2012年福建省莆田市高中毕业班教学质量检查数学试卷(理科)(解析版) 题型:解答题
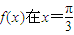 处取得极值.
处取得极值.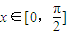 恒成立,求b的取值范围;
恒成立,求b的取值范围;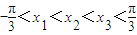 ,求证:f(sin2A+sin2C)<f(sin2B).
,求证:f(sin2A+sin2C)<f(sin2B).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com