
根据所给条件求直线的方程.
(1)直线过点(-4,0),倾斜角的正弦值为![]() ;(2)直线过点(-3,4),且在两坐标轴上的截距之和为12;
;(2)直线过点(-3,4),且在两坐标轴上的截距之和为12;
(3)直线过点(5,10),且到原点的距离为5.
|
解答 (1)由题设知,该直线的斜率存在,故可采用点斜式. 设倾斜角为α,则sinα= 从而cosα=± 则k=tanα=± 故所求直线方程为:y=± (2)由题设知截距不为0,设直线方程为 从而 故所求直线方程为:4x-y+16=0或x+3y-9=0. (3)依题设知,此直线有斜率不存在的情况. 当斜率不存在时,所求直线方程为:x-5=0; 当斜率存在时,设其为k,则y-10=k(x-5), 即kx-y+(10-5k)=0. 由点线距离公式,得 解得k= 故所求直线方程为3x-4y+25=0. 综上知,所求直线方程为x-5=0或3x-4y+25=0. 评析 求直线方程时,一方面应依据题设条件灵活选取方程的形式,另一方面应特别注意直线方程各种形式的适用范围,即注意分类讨论. |


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:高中数学 来源: 题型:
| x | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 | 3 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年山东省济宁市金乡一中高二(下)2月月考数学试卷(理科)(解析版) 题型:解答题
 .求动点P的轨迹方程.
.求动点P的轨迹方程.查看答案和解析>>
科目:高中数学 来源:2008-2009学年上海市八校高三(下)第二次联考数学试卷(理科)(解析版) 题型:解答题
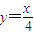 上的点,点列A1(x1,0),A2(x2,0),…,An(xn,0),…(n∈N*)顺次为x轴上的点,其中x1=a(0<a<1),对任意的n∈N*,点An、Bn、An+1构成以Bn为顶点的等腰三角形.
上的点,点列A1(x1,0),A2(x2,0),…,An(xn,0),…(n∈N*)顺次为x轴上的点,其中x1=a(0<a<1),对任意的n∈N*,点An、Bn、An+1构成以Bn为顶点的等腰三角形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com